Glosario
-
al cuadrado
Usamos la expresión al cuadrado para decir "elevado a la potencia de 2". Esta expresión viene del hecho de que un cuadrado con lados de longitud \(s\) tiene área \(s⋅s\), es decir \(s^2\).
-
aleatorio
Los resultados de un experimento de azar son aleatorios si todos son igualmente posibles.
-
ángulo llano
Un ángulo llano es un ángulo que forma una línea recta. Su medida es 180 grados.
-
ángulo recto
Un ángulo recto es la mitad de un ángulo llano. Su medida es 90 grados.
-
ángulos adyacentes
Los ángulos adyacentes comparten un lado y un vértice.
En este diagrama, el ángulo \(ABC\) es adyacente al ángulo \(DBC\).
-
ángulos opuestos
Los ángulos opuestos se forman cuando dos rectas se intersecan. Comparten un vértice y están uno frente al otro. Su medida es la misma.
Por ejemplo, los ángulos \(AEC\) y \(DEB\) son ángulos opuestos. Si el ángulo \(AEC\) mide \(120^\circ\), entonces el ángulo \(DEB\) debe medir también \(120^\circ\).
Los ángulos \(AED\) y \(BEC\) forman otro par de ángulos opuestos.
-
área
El área de una región bidimensional es el número de cuadrados unitarios que la cubre sin que queden espacios vacíos ni haya superposiciones.
Por ejemplo, el área de la región A es 8 unidades cuadradas. El área de la región sombreada de B es \(\frac12\) unidad cuadrada.
-
área de superficie
El área de superficie de un poliedro es el número de cuadrados unitarios necesarias para recubrir todas las caras del poliedro sin que queden espacios vacíos ni haya superposiciones.
Por ejemplo, si las caras de un cubo tienen 9 cm2 de área cada una, entonces el área de superficie del cubo es \(6 \boldcdot 9\), es decir 54 cm2.
-
área de un círculo
El área de un círculo cuyo radio es \(r\) unidades es \(\pi r^2\) unidades cuadradas.
Un círculo tiene radio 3 pulgadas. Su área es \(\pi3^2=9\pi\) pulgadas cuadradas, que es aproximadamente 28.3 pulgadas cuadradas.
-
aumento porcentual
Un aumento porcentual indica cuánto aumentó una cantidad, y se expresa como un porcentaje de la cantidad inicial.
Por ejemplo: El lunes, Elena tenía \$50 en el banco. El martes tenía \$56. La cantidad subió en \$6. Esto es un aumento de 12%, pues 6 es 12% de 50.
-
círculo
Un círculo consiste de todos los puntos que están a una misma distancia de un punto dado.
Por ejemplo, todo punto de este círculo está a 5 cm de distancia del punto \(A\), que es el centro del círculo.
-
circunferencia
La circunferencia de un círculo es la distancia alrededor del círculo. Si imaginas que el círculo es un pedazo de cuerda, la circunferencia es la longitud de esa cuerda. Un círculo de radio \(r\) tiene una circunferencia de \(2\pi r\).
La circunferencia de un círculo de radio 3 es \(2 \boldcdot \pi \boldcdot 3=6\pi\), que es aproximadamente 18.85.
-
complementarios
Dos ángulos son complementarios si sus medidas suman 90 grados.
Por ejemplo, un ángulo de \(15^\circ\) y un ángulo de \(75^\circ\) son complementarios.
-
constante de proporcionalidad
En una relación proporcional, los valores de una cantidad se multiplican todos por un mismo número para obtener los valores de la otra cantidad. Ese número se llama la constante de proporcionalidad.
En este ejemplo, la constante de proporcionalidad es 3, pues \(2 \boldcdot 3 = 6\), \(3 \boldcdot 3 = 9\) y \(5 \boldcdot 3 = 15\). Esto significa que, en la ensalada de frutas, hay 3 manzanas por cada 1 naranja.
número de naranjas número de manzanas 2 6 3 9 5 15 -
copia a escala
Una copia a escala es una copia de una figura en la cual cada longitud de la figura original se multiplica por el mismo número.
Por ejemplo, el triángulo \(DEF\) es una copia a escala del triángulo \(ABC\). Cada longitud de lado en el triángulo \(ABC\) fue multiplicada por 1.5 para obtener la longitud de lado correspondiente en el triángulo \(DEF\).
-
correspondiente
Si una parte de una figura y una parte de una copia de la figura están en la misma posición en relación a las demás partes de cada figura, decimos que las partes son correspondientes. Estas partes pueden ser puntos, segmentos, ángulos o distancias.
Por ejemplo, el punto en \(B\) el primer triángulo corresponde al punto \(E\) en el segundo triángulo.
El segmento \(AC\) corresponde al segmento \(DF\).
-
decimal periódico
Un decimal periódico tiene dígitos que aparecen una y otra vez, siguiendo el mismo patrón. Los dígitos que se repiten se marcan con una raya encima de ellos.
Por ejemplo, la representación decimal de \(\frac13\) es \(0.\overline{3}\), que significa 0.3333333 . . . La representación decimal de \(\frac{25}{22}\) es \(1.1\overline{36}\), que significa 1.136363636 . . .
-
depósito
Cuando pones dinero en una cuenta, esto se llama un depósito.
Por ejemplo, una persona agregó \$60 a su cuenta de banco. Antes del depósito, tenía \$435. Después del depósito, tenía \$495, porque \(435+60=495\).
-
desviación media absoluta (MAD)
La desviación media absoluta es una medida de la dispersión de un conjunto de datos. A veces la llamamos la MAD (por sus siglas en inglés). Por ejemplo, para el conjunto de datos 7, 9, 12, 13, 14, la MAD es 2.4. Esto nos dice que estos tiempos de viaje están, por lo general, a 2.4 minutos de diferencia de la media que es 11.
Para encontrar la MAD, sumamos las distancias de cada dato a la media y después dividimos entre la cantidad de datos. \(4+2+1+2+3=12\), y \(12 \div 5 = 2.4\).
-
diagrama de cinta
Un diagrama de cinta es un una colección de rectángulos que se unen para representar una relación entre cantidades.
Por ejemplo, este diagrama de cinta muestra una razón de 30 galones de pintura amarilla a 50 galones de pintura azul.
Si cada rectángulo se marcara con 5, en vez de 10, entonces la misma imagen podría representar la razón equivalente de 15 galones de pintura amarilla a 25 galones de pintura azul.
-
diámetro
Un diámetro es un segmento de recta que va desde un punto cualquiera del círculo a otro y pasa por el centro del círculo. Un diámetro puede ir en cualquier dirección. Todos los diámetros de un círculo tienen la misma longitud. También usamos la palabra diámetro para referirnos a la longitud de ese segmento.
-
dibujo a escala
Un dibujo a escala representa un lugar o un objeto. Cada medida en el dibujo corresponde a una medida del objeto real con la misma escala.
Por ejemplo, este mapa es un dibujo a escala. La escala muestra que 1 cm en el mapa representa 30 millas en la tierra.
-
disminución porcentual
Una disminución porcentual indica cuánto disminuyó una cantidad, y se expresa como un porcentaje de la cantidad inicial.
Por ejemplo: el viernes, un almacén tenía 64 sombreros en el inventario. El sábado quedaban 48 sombreros. La cantidad bajó en 16 sombreros.
Esto es una disminución de 25%, pues 16 es 25% de 64.
-
división larga
La división larga es un proceso que nos permite encontrar la forma decimal del cociente de dos números. En este proceso se va encontrando dígito a dígito, de izquierda a derecha.
Por ejemplo, este es un ejemplo del uso de la división larga para encontrar \(57 \div 4\).
\(\displaystyle \require{enclose} \begin{array}{r} 14.25 \\[-3pt] 4 \enclose{longdiv}{57.00}\kern-.2ex \\[-3pt] \underline{-4\phantom {0}}\phantom{.00} \\[-3pt] 17\phantom {.00} \\[-3pt]\underline{-16}\phantom {.00}\\[-3pt]{10\phantom{.0}} \\[-3pt]\underline{-8}\phantom{.0}\\ \phantom{0}20 \\[-3pt] \underline{-20} \\[-3pt] \phantom{00}0 \end{array} \) -
error de medición
El error de medición es la diferencia positiva entre el valor de la medición y la medida real.
Por ejemplo, Diego mide un segmento de recta y obtiene 5.3 cm. La longitud real del segmento es 5.32 cm. El error de medición es 0.02 cm, pues \(5.32−5.3=0.02\).
-
error porcentual
El error porcentual es una forma de describir el error, que se expresa como un porcentaje de la cantidad exacta.
Por ejemplo, en una caja hay 150 carpetas. Clare cuenta únicamente 147 carpetas en la caja. Esto es un error de 3 carpetas. El error porcentual es 2%, pues 3 es 2% de 150.
-
escala
Una escala nos indica la manera en la cual las medidas en un dibujo a escala representan las medidas reales del objeto.
Por ejemplo, la escala en este plano nos indica que 1 pulgada en el dibujo representa 8 pies en la alcoba verdadera. Esto significa que 2 pulgadas representan 16 pies y \(\frac12\) pulgada representa 4 pies.
-
espacio muestral
El espacio muestral es la lista de todos los resultados posibles de un experimento de azar.
Por ejemplo, el espacio muestral de lanzar dos monedas es:
cara-cara sello-cara cara-sello sello-sello -
evento
Un evento es un conjunto de uno o más resultados en un experimento de azar. Por ejemplo, al lanzar un dado numérico, hay seis resultados posibles.
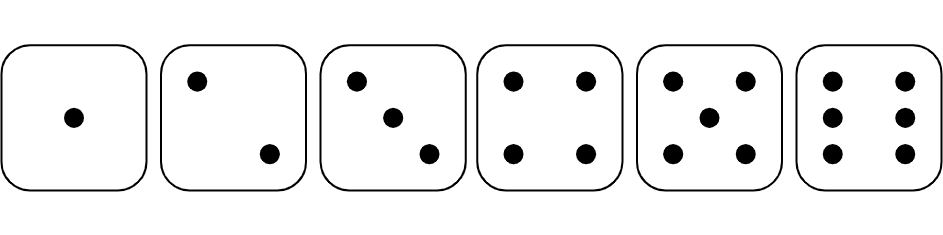
"Sacar un número menor a 3 al lanzar el dado", "sacar un número par al lanzar el dado" o "sacar 5 al lanzar el dado" son ejemplos de eventos.
-
experimento de azar
Un experimento de azar es algo que puedes hacer una y otra vez, sin saber lo que va a ocurrir cada vez.
Por ejemplo, cada vez que haces girar una ruleta, puede caer en rojo ("R"), amarillo ("Y"), azul ("B") o verde ("G").
-
expresiones equivalentes
Dos expresiones numéricas son equivalentes si tienen el mismo valor. Dos expresiones con variables son equivalentes si, al remplazar la variable por cualquier número, siempre dan el mismo valor.
Por ejemplo, \(2(7-3)+2\) es equivalente a \(\frac{35+5}{4}\), porque ambas expresiones valen 10. La expresión con variables \(3x+4x\) es equivalente a \(5x+2x\), porque sin importar qué valor le demos a \(x\), estas expresiones siempre valdrán lo mismo. Cuando \(x=3\), ambas expresiones valen 21. Cuando \(x=10\), ambas expresiones valen 70.
-
factor de escala
Para crear una copia a escala, multiplicamos todas las longitudes de la figura original por el mismo número. Ese número se llama el factor de escala.
En este ejemplo, el factor de escala es 1.5, porque \(4 \boldcdot (1.5) = 6\), \(5 \boldcdot (1.5)=7.5\), and \(6 \boldcdot (1.5)=9\).
-
media
La media es una medida de centro de un conjunto de datos. Podemos pensar en la media como un punto de equilibrio. Por ejemplo, para el conjunto de datos 7, 9, 12, 13, 14, la media es 11.
Para encontrar la media, sumamos todos los números en el conjunto de datos y después dividimos entre la cantidad de datos. \(7+9+12+13+14=55\) y \(55 \div 5 = 11\).
-
mediana
La mediana es una medida de centro de un conjunto de datos. Es el valor que queda en el medio cuando escribimos los datos en orden.
En el conjunto de datos 7, 9, 12, 13, 14, la mediana es 12.
En el conjunto de datos 3, 5, 6, 8, 11, 12, hay dos números en el medio. La mediana es 7, el promedio de estos dos números. \(6+8=14\) y \(14 \div 2=7\).
-
muestra
Una muestra es una parte de la población. Por ejemplo, si la población consiste de todos los estudiantes de séptimo grado, una muestra de esa población podría ser todos los estudiantes de séptimo grado que están en una banda.
-
número negativo
Un número negativo es un número que es menor que cero. En la recta numérica horizontal, los números negativos usualmente se muestran a la izquierda del 0.
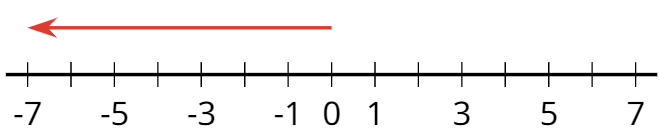
-
número positivo
Un número positivo es un número que es mayor que cero. En la recta numérica horizontal, los números positivos usualmente se muestran a la derecha del 0.
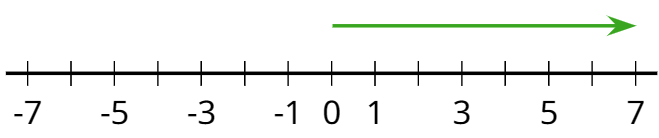
-
número racional
Un número racional es una fracción o el opuesto de una fracción.
Por ejemplo, 8 y -8 son números racionales porque se pueden escribir como \(\frac81\) y \(\text-\frac81\).
Los números 0.75 y -0.75 también son números racionales porque se pueden escribir como \(\frac{75}{100}\) y \(\text-\frac{75}{100}\).
-
origen
El origen es el punto (0,0) en el plano de coordenadas. Es el punto en el cual se intersecan el eje horizontal y el eje vertical.
-
pi ($\pi$)
Hay una relación de proporcionalidad entre el diámetro y la circunferencia de un círculo. La constante de proporcionalidad es pi. El símbolo para pi es \(\pi\).
Podemos representar esta relación con la ecuación \(C=\pi d\), donde \(C\) representa la circunferencia y \(d\) representa el diámetro.
Algunas aproximaciones de \(\pi\) son \(\frac{22}{7}\), 3.14 y 3.14159.
-
plano de coordenadas
El plano de coordenadas es un sistema para especificar la ubicación de puntos. Por ejemplo, el punto \(R\) está ubicado en \((3, 2)\) en el plano de coordenadas, porque está tres unidades a la derecha y dos unidades arriba del origen.
-
población
Una población es un conjunto de personas o cosas que queremos estudiar.
Por ejemplo, si queremos estudiar la estatura de las personas que conforman distintos equipos deportivos, la población sería todas las personas de esos equipos.
-
porcentaje
Un porcentaje es una tasa por cada 100.
Por ejemplo, una pecera puede contener 36 litros. En este momento solo hay 27 litros en la pecera. El porcentaje de la pecera que está lleno es 75%.
-
probabilidad
La probabilidad de un evento es un número que nos indica qué tan posible es que suceda ese evento. Una probabilidad de 1 indica que el evento siempre sucede. Una probabilidad de 0 indica que el evento nunca sucede.
Por ejemplo, la probabilidad de sacar una ficha de esta bolsa (de forma aleatoria) y que sea una luna es \(\frac45\).
-
proporción
Una proporción de un conjunto de datos es la fracción de los datos en una categoría dada.
Por ejemplo, una clase tiene 20 estudiantes. Hay 2 estudiantes zurdos y 18 estudiantes diestros en la clase. La proporción de estudiantes que son zurdos es \(\frac{2}{20}\), es decir 0.1.
-
radio
Un radio es un segmento de recta que va desde el centro de un círculo hasta cualquier punto del círculo. Un radio puede ir en cualquier dirección. Todos los radios de un círculo tienen la misma longitud. También usamos la palabra radio para referirnos a la longitud de ese segmento.
Por ejemplo, \(r\) es el radio de este círculo con centro \(O\).
-
rango intercuartil (IQR)
El rango intercuartil es una forma de medir qué tan dispersos están los datos. A menudo nos referimos a este como el IQR (por sus siglas en inglés). Para encontrar el rango intercuartil restamos el valor del primer cuartil del valor del tercer cuartil.
Por ejemplo, el IQR de este conjunto de datos es 20 porque \(50-30=20\).
22 29 30 31 32 43 44 45 50 50 59 Q1 Q2 Q3 -
razones equivalentes
Dos razones son equivalentes si puedes multiplicar cada uno de los números de la primera razón por el mismo factor y obtener los números de la segunda razón. Por ejemplo, \(8:6\) es equivalente a \(4:3\) porque \(8\boldcdot\frac12 = 4\) y \(6\boldcdot\frac12 = 3\).
Una receta de limonada indica que se deben usar 8 tazas de agua y 6 limones. Si usamos 4 tazas de agua y 3 limones, vamos a producir la mitad de la cantidad de limonada. Ambas recetas saben igual, porque \(8:6\) y \(4:3\) son razones equivalentes.
tazas de agua número de limones 8 6 4 3 -
recíproco
Al dividir 1 entre un número, se obtiene el recíproco de ese número. Por ejemplo, el recíproco de 12 es \(\frac{1}{12}\) y el recíproco de \(\frac25\) es \(\frac52\).
-
relación proporcional
En una relación proporcional, todos los valores de una cantidad se pueden multiplicar, cada uno por el mismo número, para obtener los valores de la otra cantidad.
Por ejemplo, en esta tabla, cada valor de \(p\) es igual a 4 veces el valor de \(s\) en la misma fila.
Podemos escribir esta relación como \(p=4s\). Esta ecuación muestra que \(p\) es proporcional a \(s\).
\(s\) \(p\) 2 8 3 12 5 20 10 40 -
representativa
Una muestra es representativa de una población si su distribución se parece a la distribución de la población (en su centro, su forma y su dispersión).
Por ejemplo, este diagrama de puntos representa una población.
Este diagrama de puntos exhibe una muestra que es representativa de la población.
-
resultado
Un resultado de un experimento de azar es una de las cosas que puede suceder cuando haces un experimento. Por ejemplo, los posibles resultados al lanzar una moneda son cara o sello.
-
retiro
Cuando retiras dinero de una cuenta, a esto se le llama un retiro.
Por ejemplo, una persona retiró \$25 de su cuenta de banco. Antes del retiro había \$350. Después del retiro había \$325, porque \(350−25=325\).
-
sección transversal
Una sección transversal es la nueva cara que ves cuando le haces un corte a una figura tridimensional.
Por ejemplo, si tomas una pirámide rectangular y le haces un corte paralelo a la base, la sección transversal que obtienes es un rectángulo más pequeño.
-
simulación
Una simulación es un experimento que se usa para estimar la probabilidad de un evento del mundo real.
Por ejemplo, supongamos que el pronóstico del tiempo dice que hay una probabilidad de 25% de lluvia. Podemos simular esta situación con una ruleta con cuatro secciones iguales. Si la ruleta cae en rojo, esto representa que llovió. Si la ruleta cae en cualquier otro color, esto representa que no llovió.
-
solución de una ecuación
Una solución de una ecuación es un número que al reemplazar a la variable hace que la ecuación sea verdadera.
Por ejemplo, 7 es la solución de la ecuación \(m+1=8\), porque \(7+1=8\) es cierto. En cambio, 9 no es solución de \(m+1=8\), porque \(9+1\ne8\).
-
suplementarios
Dos ángulos son suplementarios si sus medidas suman 180 grados.
Por ejemplo, un ángulo de \(15^\circ\) y un ángulo de \(165^\circ\) son suplementarios.
-
tasa unitaria
Una tasa unitaria es una tasa por cada 1.
Por ejemplo, 12 personas comparten 2 tartas de manera equitativa. Una tasa unitaria es 6 personas por cada tarta, porque \(12 \div 2 = 6\). La otra tasa unitaria es \(\frac16\) de tarta por cada persona, porque \(2 \div 12 = \frac16\).
-
valor absoluto
El valor absoluto de un número es su distancia al 0 en la recta numérica.
El valor absoluto de -7 es 7, porque -7 está a 7 unidades del 0. El valor absoluto de 5 es 5, porque 5 está a 5 unidades del 0.
-
variable
Una variable es una letra que representa un número. Puedes elegir distintos números como valores de la variable.
Por ejemplo, en la expresión \(10-x\), la variable es \(x\). Si el valor de \(x\) es 3, entonces \(10-x=7\), porque \(10-3=7\). Si el valor de \(x\) es 6, entonces \(10-x=4\), porque \(10-6=4\).