Glosario
-
ángulo llano
Un ángulo llano es un ángulo que forma una línea recta. Su medida es 180 grados.
-
ángulo recto
Un ángulo recto es la mitad de un ángulo llano. Su medida es 90 grados.
-
ángulos alternos internos
Los ángulos alternos internos se crean cuando una recta (llamada una transversal) cruza a dos rectas paralelas. Los ángulos alternos internos están en la franja que se forma entre las dos rectas paralelas y en lados opuestos de la transversal.
Este diagrama muestra dos pares de ángulos alternos internos. Los ángulos \(a\) y \(d\) son un par, y los ángulos \(b\) y \(c\) son otro.
-
ángulos opuestos
Los ángulos opuestos se forman cuando dos rectas se intersecan. Comparten un vértice y están uno frente al otro. Su medida es la misma.
Por ejemplo, los ángulos \(AEC\) y \(DEB\) son ángulos opuestos. Si el ángulo \(AEC\) mide \(120^\circ\), entonces el ángulo \(DEB\) debe medir también \(120^\circ\).
Los ángulos \(AED\) y \(BEC\) forman otro par de ángulos opuestos.
-
asociación negativa
Una asociación negativa es una relación entre dos cantidades en la cual una tiende a disminuir cuando la otra aumenta. En un diagrama de dispersión, los puntos de datos tienden a agruparse alrededor de una recta con pendiente negativa.
Distintas tiendas en el país venden un libro a distintos precios.
El diagrama de dispersión muestra que hay una asociación negativa entre el precio del libro (en dólares) y el número de libros vendidos a ese precio.
-
asociación positiva
Una asociación positiva es una relación entre dos cantidades en la cual una tiende a aumentar cuando la otra aumenta. En un diagrama de dispersión, los puntos de datos tienden a agruparse alrededor de una recta con pendiente positiva.
La relación entre la altura y el peso de 25 perros se muestra en este diagrama de dispersión. Hay una asociación positiva entre la altura del perro y el peso del perro.
-
base (de un exponente)
En expresiones como \(5^3\) y \(8^2\), el 5 y el 8 se llaman bases. Esta indica qué factor se va a multiplicar repetidamente. Por ejemplo, \(5^3\) = \(5 \boldcdot 5 \boldcdot 5\) y \(8^2 = 8 \boldcdot 8\).
-
cateto
Los catetos de un triángulo rectángulo son los lados que forman el ángulo recto.
Estos son algunos triángulos rectángulos. Cada cateto está etiquetado.
-
centro de una dilatación
El centro de una dilatación es un punto fijo en un plano. Es el punto desde el cual medimos las distancias en una dilatación.
En este diagrama, el punto \(P\) es el centro de la dilatación.
-
cilindro
Un cilindro es una figura tridimensional parecida a un prisma, pero con bases que son círculos.
-
coeficiente
El coeficiente de una variable es el número que la multiplica.
Por ejemplo, en la expresión \(3x+5\), el coeficiente de la \(x\) es 3. En la expresión \(y+5\), el coeficiente de la \(y\) es 1, porque \(y=1 \boldcdot y\). En la expresión \(\frac{3x}{4}-2\) el coeficiente de la \(x\) es \(\frac34\), porque \(\frac{3x}{4}=\frac34 \boldcdot x\).
-
congruente
Una figura es congruente a otra si puede moverse con traslaciones, rotaciones y reflexiones para coincidir exactamente con la otra.
En la figura, el triángulo A es congruente a los triángulos B, C y D. Una traslación lleva al triángulo A al triángulo B, una rotación lleva el triángulo B al triángulo C, y una reflexión lleva el triángulo C al triángulo D.
-
cono
Un cono es una figura tridimensional parecida a una pirámide, pero con base circular.
-
constante de proporcionalidad
En una relación proporcional, los valores de una cantidad se multiplican todos por un mismo número para obtener los valores de la otra cantidad. Ese número se llama la constante de proporcionalidad.
En este ejemplo, la constante de proporcionalidad es 3, pues \(2 \boldcdot 3 = 6\), \(3 \boldcdot 3 = 9\) y \(5 \boldcdot 3 = 15\). Esto significa que, en la ensalada de frutas, hay 3 manzanas por cada 1 naranja.
número de naranjas número de manzanas 2 6 3 9 5 15 -
correspondiente
Si una parte de una figura y una parte de una copia de la figura están en la misma posición en relación a las demás partes de cada figura, decimos que las partes son correspondientes. Estas partes pueden ser puntos, segmentos, ángulos o distancias.
Por ejemplo, el punto en \(B\) el primer triángulo corresponde al punto \(E\) en el segundo triángulo.
El segmento \(AC\) corresponde al segmento \(DF\).
-
dato atípico
Un dato atípico es un dato que está lejos de los demás datos en un conjunto de datos.
Este es un diagrama de dispersión que muestra largos y anchos de 20 pies izquierdos distintos. El pie con 24.5 cm de largo y 7.8 cm de ancho es un dato atípico.
-
decimal periódico
Un decimal periódico tiene dígitos que aparecen una y otra vez, siguiendo el mismo patrón. Los dígitos que se repiten se marcan con una raya encima de ellos.
Por ejemplo, la representación decimal de \(\frac13\) es \(0.\overline{3}\), que significa 0.3333333 . . . La representación decimal de \(\frac{25}{22}\) es \(1.1\overline{36}\), que significa 1.136363636 . . .
-
diagrama de dispersión
Un diagrama de dispersión es un gráfico que muestra los valores de dos variables en un plano de coordenadas. Permite investigar conexiones entre las dos variables.
En este diagrama, cada punto corresponde a uno de 25 perros. Las coordenadas de cada punto indican la altura y el peso de ese perro.
-
dilatación
Una dilatación es una transformación en la cual cada punto de una figura cambia su distancia a un punto fijo al moverse sobre la recta que pasa por el punto fijo. El punto fijo es el centro de la dilatación. Todas las distancias originales se multiplican por el mismo factor de escala.
Por ejemplo, el triángulo \(DEF\) es una dilatación del triángulo \(ABC\). El centro de la dilatación es \(O\) y el factor de escala es 3.
Esto significa que todos los puntos del triángulo \(DEF\) están 3 veces tan lejos de \(O\) como todos los puntos correspondientes del triángulo \(ABC\).
-
en el sentido contrario a las manecillas del reloj
En el sentido contrario a las manecillas del reloj significa que se gira en la dirección opuesta a la dirección en la cual giran las manecillas de un reloj. Así, un punto que está encima del centro de rotación gira hacia la izquierda.
Este diagrama muestra como la figura A gira en el sentido contrario a las manecillas del reloj para formar a la figura B.
-
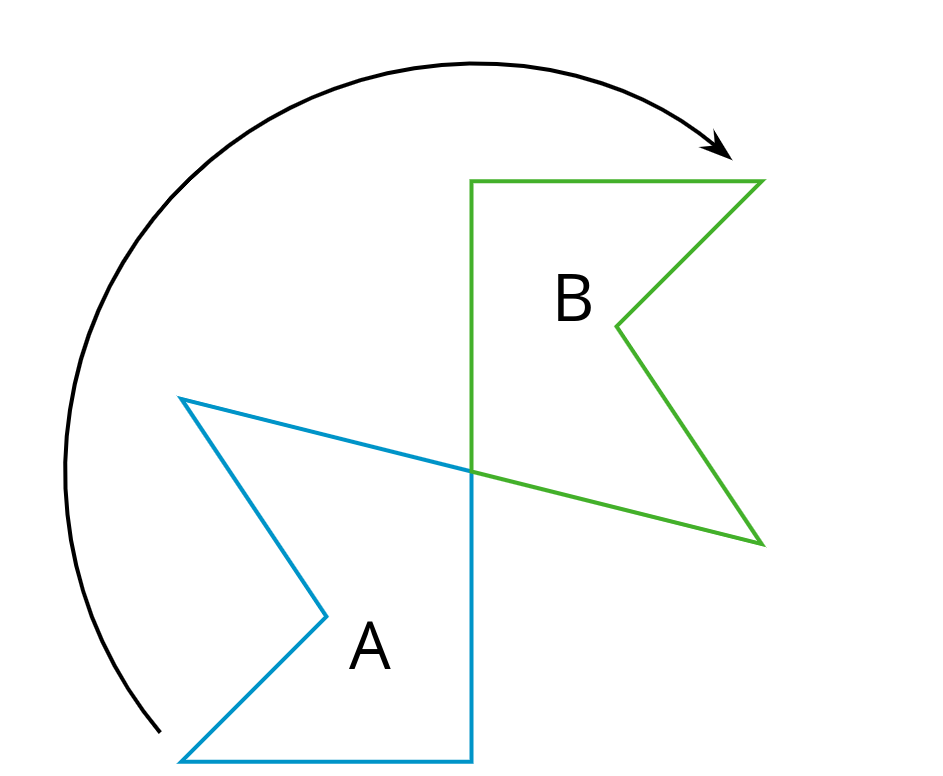
en el sentido de las manecillas del reloj
En el sentido de las manecillas del reloj significa que se gira en la misma dirección que giran las manecillas de un reloj. Así, un punto que está encima del centro de rotación gira hacia la derecha. Este diagrama muestra como la figura A se giró en el sentido de las manecillas del reloj para formar la figura B.
-
esfera
Una esfera es una figura tridimensional cuyas secciones transversales, en cualquier dirección, son círculos.
-
exponente
En expresiones como \(5^3\) y \(8^2\), el 3 y el 2 se llaman exponentes. Estos nos indican cuántas veces multiplicar cada número por sí mismo. Por ejemplo, \(5^3\) = \(5 \boldcdot 5 \boldcdot 5\) y \(8^2 = 8 \boldcdot 8\).
-
factor de escala
Para crear una copia a escala, multiplicamos todas las longitudes de la figura original por el mismo número. Ese número se llama el factor de escala.
En este ejemplo, el factor de escala es 1.5, porque \(4 \boldcdot (1.5) = 6\), \(5 \boldcdot (1.5)=7.5\), and \(6 \boldcdot (1.5)=9\).
-
frecuencia relativa
La frecuencia relativa de una categoría indica la proporción en la cual esa categoría ocurre en un conjunto de datos. Se representa como una fracción, un decimal o un porcentaje del número total.
Había 21 perros en el parque. Algunos eran de color blanco, otros de color marrón, otros de color negro y otros eran multicolor. La tabla muestra la frecuencia y la frecuencia relativa de cada color.
color frecuencia frecuencia relativa blanco 5 \(\frac{5}{21}\) marrón 7 \(\frac{7}{21}\) negro 3 \(\frac{3}{21}\) multicolor 6 \(\frac{6}{21}\) -
función
Una función es una regla que asigna exactamente una salida a cada posible entrada.
La función \(y=6x+4\) asigna un valor de salida, \(y\), a cada valor de entrada, \(x\). Por ejemplo, cuando \(x=5\), entonces \(y=6(5)+4\), es decir 34.
-
gráfico de barras segmentadas
Un gráfico de barras segmentadas permite comparar dos categorías dentro de un conjunto de datos. La barra completa representa todos los datos dentro de una misma categoría. Cada barra está separada en partes (segmentos) que muestran el porcentaje de cada parte dentro de la categoría.
-
hipotenusa
En un triángulo rectángulo, la hipotenusa es el lado que está opuesto al ángulo recto. Es el lado más largo del triángulo rectángulo.
Estos son algunos triángulos rectángulos. Cada hipotenusa está etiquetada.
-
imagen
Una imagen es el resultado de aplicar traslaciones, rotaciones y reflexiones a un objeto. Cada parte del objeto original se mueve de la misma manera para coincidir con la parte correspondiente de la imagen.
En este diagrama, el triángulo \(ABC\) fue trasladado hacia arriba y hacia la derecha para forma el triángulo \(DEF\). El triángulo \(DEF\) es la imagen del triángulo original \(ABC\).
-
intersección con el eje vertical
La intersección con el eje vertical es el punto en el cual la gráfica de una recta cruza el eje vertical
La intersección con el eje vertical de esta recta es \((0,\text-6)\) o simplemente -6.
-
notación científica
La notación científica es una forma de escribir números muy grandes o muy pequeños. Para escribir un número en notación científica, lo escribimos como la multiplicación de un número entre 1 y 10 por una potencia de 10.
Por ejemplo, el número 425,000,000 en notación científica es \(4.25 \times 10^8\). El número 0.0000000000783 en notación científica es \(7.83 \times 10^{\text-11}\).
-
número irracional
Un número irracional es un número que no es una fracción ni el opuesto de una fracción.
Pi (\(\pi\)) y \(\sqrt{2}\) son ejemplos de números irracionales.
-
número racional
Un número racional es una fracción o el opuesto de una fracción.
Algunos ejemplos de números racionales son: \(\frac74, 0, \frac63, 0.2, \text-\frac13,\text-5,\sqrt9\)
-
pendiente
La pendiente de una recta es un número que podemos calcular usando cualesquiera dos puntos de la recta. Para ello, primero consideramos la distancia vertical entre ellos y la distancia horizontal entre ellos; la pendiente se halla al dividir la distancia vertical entre la distancia horizontal.
La pendiente de esta recta es 2 dividido entre 3, es decir \(\frac23\).
-
plano de coordenadas
El plano de coordenadas es un sistema para especificar la ubicación de puntos. Por ejemplo, el punto \(R\) está ubicado en \((3, 2)\) en el plano de coordenadas, porque está tres unidades a la derecha y dos unidades arriba del origen.
-
radio
Un radio es un segmento de recta que va desde el centro de un círculo hasta cualquier punto del círculo. Un radio puede ir en cualquier dirección. Todos los radios de un círculo tienen la misma longitud. También usamos la palabra radio para referirnos a la longitud de ese segmento.
Por ejemplo, \(r\) es el radio de este círculo con centro \(O\).
-
raíz cuadrada
La raíz cuadrada de un número positivo \(n\) es el número positivo que al ser elevado al cuadrado da \(n\). También es la longitud de lado de un cuadrado de área \(n\). Escribimos la raíz cuadrada de \(n\) como \(\sqrt{n}\).
Por ejemplo, la raíz cuadrada de 16, que se escribe como \(\sqrt{16}\), es 4 pues \(4^2\) es 16.
\(\sqrt{16}\) también es la longitud de lado de un cuadrado que tiene un área de 16.
-
raíz cúbica
La raíz cúbica de un número \(n\) es el número que al ser elevado al cubo da \(n\). También es la longitud de una arista de un cubo que tiene volumen \(n\). Escribimos la raíz cúbica de \(n\) como \(\sqrt[3]{n}\).
Por ejemplo, la raíz cúbica de 64, que se escribe como \(\sqrt[3]{64}\), es 4 porque \(4^3\) es 64.
\(\sqrt[3]{64}\) también es la longitud de una arista de un cubo que tiene un volumen de 64.
-
recíproco
Al dividir 1 entre un número, se obtiene el recíproco de ese número. Por ejemplo, el recíproco de 12 es \(\frac{1}{12}\) y el recíproco de \(\frac25\) es \(\frac52\).
-
reflexión
Una reflexión con respecto a una recta toma cada punto de una figura y lo mueve de manera perpendicular a un punto que está ubicado al lado opuesto de esa recta. El nuevo punto está a la misma distancia de la recta que el punto original.
Este diagrama muestra una reflexión de A con respecto a la recta \(\ell\) que produce la figura imagen B.
-
relación lineal
Que haya una relación lineal entre dos cantidades significa que se relacionan así: siempre que una cantidad cambia en una cierta cantidad, la otra cantidad cambia en otra cantidad fija. En una relación lineal, una cantidad tiene una tasa de cambio constante con respecto a la otra.
La relación se llama lineal pues su gráfica es una línea recta.
Esta gráfica muestra una relación entre el número de días y el número de páginas leídas.
Siempre que el número de días aumenta en 2, el número de páginas leídas aumenta en 60. La tasa de cambio es constante, 30 páginas por día. Por lo tanto, la relación es lineal.
-
rotación
Una rotación hace girar cada punto de una figura alrededor de un centro con un ángulo dado en una dirección específica.
Este diagrama muestra como al rotar el triángulo A alrededor del centro \(O\) con un ángulo de 55 grados en la dirección de las manecillas del reloj, se obtiene el triángulo B.
-
secuencia de transformaciones
Una secuencia de transformaciones es un conjunto de traslaciones, rotaciones, reflexiones y dilataciones de una figura, que se realizan en un orden dado.
Este diagrama muestra una secuencia de transformaciones que lleva la figura A a la figura C.
Primero, A se traslada hacia la derecha para formar B. Luego, B se refleja con respecto a la recta \(\ell\) para formar C.
-
semejantes
Dos figuras son semejantes si una se puede hacer coincidir exactamente con la otra, al realizar una secuencia de transformaciones rígidas y dilataciones.
En esta figura, el triángulo \(ABC\) es semejante al triángulo \(DEF\).
Si \(ABC\) se rota alrededor del punto \(B\) y luego se dilata con centro \(O\), entonces va a coincidir exactamente con \(DEF\). Esto significa que son semejantes.
-
sistema de ecuaciones
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones. Cada ecuación contiene dos o más variables. Queremos encontrar valores para las variables que hagan que todas las ecuaciones del sistema sean verdaderas.
Estas ecuaciones forman un sistema de ecuaciones:
\(\displaystyle \begin{cases} x + y = \text-2\\x - y = 12\end{cases}\)
La solución de este sistema es \(x=5\) y \(y=\text-7\) porque cuando remplazamos las variables \(x\) y \(y\) por esos valores, ambas ecuaciones son verdaderas: \(5+(\text-7)=\text-2\) y \(5-(\text-7)=12\).
-
solución de una ecuación en dos variables
Una solución de una ecuación en dos variables es una pareja de valores para las variables que hacen que la ecuación sea verdadera.
Por ejemplo, una posible solución de la ecuación \(4x+3y=24\) es \((6,0)\). Al remplazar \(x\) por 6 y \(y\) por 0, la ecuación es verdadera porque \(4(6)+3(0)=24\).
-
tabla de doble entrada
Una tabla de doble entrada nos permite comparar dos variables categóricas.
Esta muestra a una de las variables en las columnas y a la otra variable en las filas. Cada entrada en la tabla es la frecuencia o la frecuencia relativa de la categoría que definen los encabezados de esa columna y esa fila.
Un estudio investiga la conexión entre la meditación y el estado de ánimo de los atletas antes de una competencia. Esta tabla de doble entrada muestra los resultados del estudio.
meditó no meditó total calmado 45 8 53 agitado 23 21 44 total 68 29 97 -
tasa de cambio
La tasa de cambio en una relación lineal entre \(x\) y \(y\), es la cantidad que \(y\) cambia cuando \(x\) aumenta en 1. La tasa de cambio en una relación lineal también es la pendiente de su gráfica.
En esta gráfica, \(y\) aumenta en 15 dólares cuando \(x\) aumenta en 1 hora. La tasa de cambio es 15 dólares por hora.
-
teorema de Pitágoras
El teorema de Pitágoras describe la relación entre las longitudes de los lados de un triángulo rectángulo.
Es diagrama muestra un triángulo rectángulo con cuadrados construidos en cada lado. Si sumamos las áreas de los dos cuadrados más pequeños, obtenemos el área del cuadrado grande.
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Esto se escribe como \(a^2+b^2=c^2\).
-
término
Un término es una parte de una expresión. Puede ser un solo número, una variable, o la multiplicación de un número con una variable. Por ejemplo, la expresión \(5x + 18\)tiene dos términos: el primer término es \(5x\) y el segundo término es 18.
-
término constante
En la expresión \(5x + 2\) hay dos términos: \(5x\) y 2. El número 2 se llama el término constante pues no cambia cuando \(x\) cambia.
En la expresión \(7x+9\), 9 es el término constante.
En la expresión \(5x+(\text-8)\), -8 es el término constante.
En la expresión \(12-4x\), 12 es el término constante. -
teselación
Una teselación es un patrón repetido de una o más figuras. Los lados de las figuras coinciden perfectamente y no se superponen. El patrón se repite eternamente en todas las direcciones.
Este diagrama muestra parte de una teselación.
-
transformación
Una transformación es una traslación, una rotación, una reflexión, una dilatación o una combinación de ellas.
-
transformación rígida
Una transformación rígida es una movida del plano que no cambia ninguna de las medidas de una figura. Traslaciones, rotaciones y reflexiones (o cualquier secuencia de ellas) son transformaciones rígidas.
-
transversal
Una transversal es una recta que cruza dos rectas paralelas.
Este diagrama muestra una recta transversal, \(k\), que cruza a dos rectas paralelas, \(m\) y \(\ell\).
-
traslación
Una traslación mueve cada punto de una figura cierta distancia en cierta dirección.
Este diagrama muestra cómo la figura A se traslada para obtener la figura B usando la dirección y la distancia indicadas por la flecha.
-
variable dependiente
Una variable dependiente representa la salida de una función.
Vamos a comprar 20 frutas y decidimos que serán manzanas y bananos. Si elegimos el número "\(a\)" de manzanas primero, la ecuación \(b=20-a\) nos dice el número "\(b\)" de bananos que podemos comprar. El número de bananos es la variable dependiente porque depende del número de manzanas.
-
variable independiente
Una variable independiente es una cantidad que se usa para calcular otra cantidad. Una variable independiente representa la entrada de una función.
Vamos a comprar 20 frutas y decidimos que serán manzanas y bananos. Si elegimos el número "\(a\)" de manzanas primero, la ecuación \(b=20-a\) nos dice el número "\(b\)" de bananos que podemos comprar. El número de manzanas es la variable independiente porque podemos elegir cualquier número como su valor.
-
vértice
Un vértice es un punto en donde dos o más aristas se encuentran. Los vértices de este polígono están etiquetados con las letras \(A\), \(B\), \(C\), \(D\) y \(E\).
-
volumen
El volumen de una región tridimensional es el número de unidades cúbicas que la llenan, sin espacios ni superposiciones.
Por ejemplo, el volumen de este prisma rectangular es 60 unidades3, pues está compuesto por 3 capas, cada una de 20 unidades3.