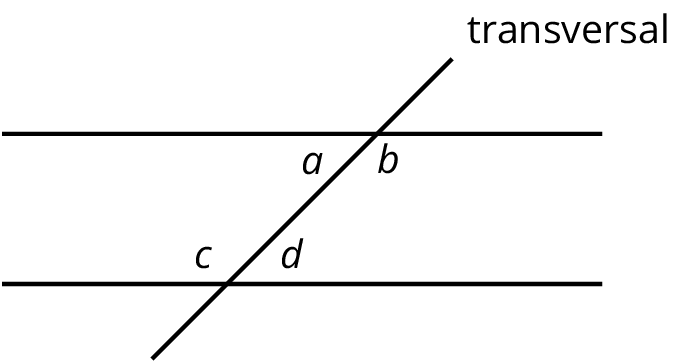
If two interior angles lie on opposite sides of the transversal they are called alternate interior angles.
In the figure, \(a\) and \(d\) are alternate interior angles, and \(b\) and \(c\) are also alternate interior angles.
Interior angles are angles that are made by a transversal crossing two parallel lines. They are the angles that lie between the parallel lines, not outside them.
If two interior angles lie on opposite sides of the transversal they are called alternate interior angles.
In the figure, \(a\) and \(d\) are alternate interior angles, and \(b\) and \(c\) are also alternate interior angles.
In expressions like \(5^3\) and \(8^2\), the 5 and the 8 are called bases. They tell you what factor to multiply repeatedly. For example, \(5^3\) = \(5 \boldcdot 5 \boldcdot 5\), and \(8^2 = 8 \boldcdot 8\).
The word base can also refer to a face of a polyhedron.
A prism has two identical bases that are parallel. A pyramid has one base.
A prism or pyramid is named for the shape of its base.
Description: <p>The figure on the left is labeled pentagonal prism. There are two identical pentagons on the top and bottom. Each vertex of a pentagon is connected by a vertical segment to the corresponding vertex of the other pentagons. The pengatons are each shaded, with the word base pointing to each. The figure on the right is labeled hexagonal pyramid. There is a hexagon on the bottom shaded green. From a point above the hexagon extend 6 segments, each connected to a vertex of the hexagon.</p>
The center of a dilation is a fixed point on a plane. It is the starting point from which we measure distances in a dilation.
In this diagram, point \(P\) is the center of the dilation.
Clockwise means to turn in the same direction as the hands of a clock. The top turns to the right. This diagram shows Figure A turned clockwise to make Figure B.
A coefficient is a number that is multiplied by a variable.
For example, in the expression \(3x+5\), the coefficient of \(x\) is 3. In the expression \(y+5\), the coefficient of \(y\) is 1, because \(y=1 \boldcdot y\).
Complementary angles have measures that add up to 90 degrees.
For example, a \(15^\circ\) angle and a \(75^\circ\) angle are complementary.
A cone is a three-dimensional figure like a pyramid, but the base is a circle.
One figure is congruent to another if it can be moved with translations, rotations, and reflections to fit exactly over the other.
In the figure, Triangle A is congruent to Triangles B, C, and D. A translation takes Triangle A to Triangle B, a rotation takes Triangle B to Triangle C, and a reflection takes Triangle C to Triangle D.
In a proportional relationship, the values for one quantity are each multiplied by the same number to get the values for the other quantity. This number is called the constant of proportionality.
In this example, the constant of proportionality is 3, because \(2 \boldcdot 3 = 6\), \(3 \boldcdot 3 = 9\), and \(5 \boldcdot 3 = 15\). This means that there are 3 apples for every 1 orange in the fruit salad.
| number of oranges | number of apples |
|---|---|
| 2 | 6 |
| 3 | 9 |
| 5 | 15 |
In an expression like \(5x+2\), the number 2 is called the constant term because it doesn’t change when \(x\) changes.
In the expression \(7x+9\), 9 is the constant term.
In the expression \(5x+(\text-8)\), -8 is the constant term.
In the expression \(12-4x\), 12 is the constant term.
The coordinate plane is a system for telling where points are. For example. point \(R\) is located at \((3, 2)\) on the coordinate plane, because it is three units to the right and two units up.
When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.
For example, point \(B\) in the first triangle corresponds to point \(E\) in the second triangle. Segment \(AC\) corresponds to segment \(DF\).
Counterclockwise means to turn opposite of the way the hands of a clock turn. The top turns to the left.
This diagram shows Figure A turned counterclockwise to make Figure B.
A cross section is the new face you see when you slice through a three-dimensional figure.
For example, if you slice a rectangular pyramid parallel to the base, you get a smaller rectangle as the cross section.
The cube root of a number \(n\) is the number whose cube is \(n\). It is also the edge length of a cube with a volume of \(n\). We write the cube root of \(n\) as \(\sqrt[3]{n}\).
For example, the cube root of 64, written as \(\sqrt[3]{64}\), is 4 because \(4^3\) is 64. \(\sqrt[3]{64}\) is also the edge length of a cube that has a volume of 64.
A cylinder is a three-dimensional figure like a prism, but with bases that are circles.
A dependent variable represents the output of a function.
For example, suppose we need to buy 20 pieces of fruit and decide to buy apples and bananas. If we select the number of apples first, the equation \(b=20-a\) shows the number of bananas we can buy. The number of bananas is the dependent variable because it depends on the number of apples.
A dilation with center \(O\) and positive scale factor \(r\) takes a point \(P\) along the line \(OP\) to another point whose distance is \(r\) times further away from \(O\) than \(P\) is. If \(r < 1\) then the new point is really closer to \(O\), not further away.
The triangle \(DEF\) is a dilation of the triangle \(ABC\) with center \(O\) and with scale factor 3. So \(D\) is 3 times further away from \(O\) than \(A\) is, \(E\) is 3 times further away from \(O\) than \(B\) is, and \(F\) is 3 times further away from \(O\) than \(C\) is.

Equivalent expressions are always equal to each other. If the expressions have variables, they are equal whenever the same value is used for the variable in each expression.
For example, \(3x+4x\) is equivalent to \(5x+2x\). No matter what value we use for \(x\), these expressions are always equal. When \(x\) is 3, both expressions equal 21. When \(x\) is 10, both expressions equal 70.
To expand an expression, we use the distributive property to rewrite a product as a sum. The new expression is equivalent to the original expression.
For example, we can expand the expression \(5(4x+7)\) to get the equivalent expression \(20x + 35\).
In expressions like \(5^3\) and \(8^2\), the 3 and the 2 are called exponents. They tell you how many factors to multiply. For example, \(5^3\) = \(5 \boldcdot 5 \boldcdot 5\), and \(8^2 = 8 \boldcdot 8\).
To factor an expression, we use the distributive property to rewrite a sum as a product. The new expression is equivalent to the original expression.
For example, we can factor the expression \(20x + 35\) to get the equivalent expression \(5(4x+7)\).
A function is a rule that assigns exactly one output to each possible input.
The function \(y=6x+4\) assigns one value of the output, \(y\), to each value of the input, \(x\). For example, when \(x\) is 5, then \(y=6(5)+4\) or 34.
The hypotenuse is the side of a right triangle that is opposite the right angle. It is the longest side of a right triangle.
Here are some right triangles. Each hypotenuse is labeled.
An image is the result of translations, rotations, and reflections on an object. Every part of the original object moves in the same way to match up with a part of the image.
In this diagram, triangle \(ABC\) has been translated up and to the right to make triangle \(DEF\). Triangle \(DEF\) is the image of the original triangle \(ABC\).
An independent variable represents the input of a function.
For example, suppose we need to buy 20 pieces of fruit and decide to buy some apples and bananas. If we select the number of apples first, the equation \(b=20-a\) shows the number of bananas we can buy. The number of apples is the independent variable because we can choose any number for it.
An irrational number is a number that is not a fraction or the opposite of a fraction.
Pi (\(\pi\)) and \(\sqrt2\) are examples of irrational numbers.
The legs of a right triangle are the sides that make the right angle.
Here are some right triangles. Each leg is labeled.
A linear relationship between two quantities means they are related like this: When one quantity changes by a certain amount, the other quantity always changes by a set amount. In a linear relationship, one quantity has a constant rate of change with respect to the other.
The relationship is called linear because its graph is a line.
The graph shows a relationship between number of days and number of pages read.
When the number of days increases by 2, the number of pages read always increases by 60. The rate of change is constant, 30 pages per day, so the relationship is linear.
A negative association is a relationship between two quantities where one tends to decrease as the other increases. In a scatter plot, the data points tend to cluster around a line with negative slope.
Different stores across the country sell a book for different prices.
The scatter plot shows that there is a negative association between the the price of the book in dollars and the number of books sold at that price.
An outlier is a data value that is far from the other values in the data set.
Here is a scatter plot that shows lengths and widths of 20 different left feet. The foot whose length is 24.5 cm and width is 7.8 cm is an outlier.
Description: <p>A scatterplot. Horizontal, from 20 to 32, by 2's, labeled foot length in centimeters. Vertical, from 7 to 12, by 1’s, labeled foot width in centimeters. 20 dots trend upward and to the right. Line drawn, trends linearly upward and right with 11 dots above lie and 9 below. No dots lie on the line. The line begins at about point 21 point 9 comma 9 and ends at about 31 point 25 comma 11 point 5.</p>
A positive association is a relationship between two quantities where one tends to increase as the other increases. In a scatter plot, the data points tend to cluster around a line with positive slope.
The relationship between height and weight for 25 dogs is shown in the scatter plot. There is a positive association between dog height and dog weight.
A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.
Here are some drawings of prisms.
A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.
Here are some drawings of pyramids.
The Pythagorean Theorem describes the relationship between the side lengths of right triangles.
The diagram shows a right triangle with squares built on each side. If we add the areas of the two small squares, we get the area of the larger square.
The square of the hypotenuse is equal to the sum of the squares of the legs. This is written as \(a^2+b^2=c^2\).
A radius is a line segment that goes from the center to the edge of a circle. A radius can go in any direction. Every radius of the circle is the same length. We also use the word radius to mean the length of this segment.
For example, \(r\) is the radius of this circle with center \(O\).
The rate of change in a linear relationship is the amount \(y\) changes when \(x\) increases by 1. The rate of change in a linear relationship is also the slope of its graph.
In this graph, \(y\) increases by 15 dollars when \(x\) increases by 1 hour. The rate of change is 15 dollars per hour.
Description: <p>graph, horizontal axis, time in hours, scale 0 to 9, by 1's. vertical axis, amount earned in dollars, scale 0 to 140, by 20's. line starting at 0 comma 10, passing through 2 comma 40 and 60 comma 100.</p>
A rational number is a fraction or the opposite of a fraction.
Some examples of rational numbers are: \(\frac74,0,\frac63,0.2,\text-\frac13,\text-5,\sqrt9\)
Dividing 1 by a number gives the reciprocal of that number. For example, the reciprocal of 12 is \(\frac{1}{12}\), and the reciprocal of \(\frac25\) is \(\frac52\).
A reflection across a line moves every point on a figure to a point directly on the opposite side of the line. The new point is the same distance from the line as it was in the original figure.
This diagram shows a reflection of A over line \(\ell\) that makes the mirror image B.
The relative frequency of a category tells us the proportion at which the category occurs in the data set. It is expressed as a fraction, a decimal, or a percentage of the total number.
For example, suppose there were 21 dogs in the park, some white, some brown, some black, and some multi-color. The table shows the frequency and the relative frequency of each color.
| color | frequency | relative frequency |
|---|---|---|
| white | 5 | \(\frac{5}{21}\) |
| brown | 7 | \(\frac{7}{21}\) |
| black | 3 | \(\frac{3}{21}\) |
| multi-color | 6 | \(\frac{6}{21}\) |
A repeating decimal has digits that keep going in the same pattern over and over. The repeating digits are marked with a line above them.
For example, the decimal representation for \(\frac13\) is \(0.\overline{3}\), which means 0.3333333 . . . The decimal representation for \(\frac{25}{22}\) is \(1.1\overline{36}\) which means 1.136363636 . . .
A right angle is half of a straight angle. It measures 90 degrees.
A rigid transformation is a move that does not change any measurements of a figure. Translations, rotations, and reflections are rigid transformations, as is any sequence of these.
A rotation moves every point on a figure around a center by a given angle in a specific direction.
This diagram shows Triangle A rotated around center \(O\) by 55 degrees clockwise to get Triangle B.
A scale tells how the measurements in a scale drawing represent the actual measurements of the object.
For example, the scale on this floor plan tells us that 1 inch on the drawing represents 8 feet in the actual room. This means that 2 inches would represent 16 feet, and \(\frac12\) inch would represent 4 feet.
A scaled copy is a copy of a figure where every length in the original figure is multiplied by the same number.
For example, triangle \(DEF\) is a scaled copy of triangle \(ABC\). Each side length on triangle \(ABC\) was multiplied by 1.5 to get the corresponding side length on triangle \(DEF\).
A scale drawing represents an actual place or object. All the measurements in the drawing correspond to the measurements of the actual object by the same scale.
To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.
In this example, the scale factor is 1.5, because \(4 \boldcdot (1.5) = 6\), \(5 \boldcdot (1.5)=7.5\), and \(6 \boldcdot (1.5)=9\).
A scatter plot is a graph that shows the values of two variables on a coordinate plane. It allows us to investigate connections between the two variables.
Each plotted point corresponds to one dog. The coordinates of each point tell us the height and weight of that dog.
Scientific notation is a way to write very large or very small numbers. We write these numbers by multiplying a number between 1 and 10 by a power of 10.
For example, the number 425,000,000 in scientific notation is \(4.25 \times 10^8\). The number 0.0000000000783 in scientific notation is \(7.83 \times 10^{\text-11}\).
A segmented bar graph compares two categories within a data set. The whole bar represents all the data within one category. Then, each bar is separated into parts (segments) that show the percentage of each part in the second category.
This segmented bar graph shows the percentage of people in different age groups that do and do not have a cell phone. For example, among people ages 10 to 12, about 40% have a cell phone and 60% do not have a cell phone.
A sequence of transformations is a set of translations, rotations, reflections, and dilations on a figure. The transformations are performed in a given order.
This diagram shows a sequence of transformations to move Figure A to Figure C.
First, A is translated to the right to make B. Next, B is reflected across line \(\ell\) to make C.
Two figures are similar if one can fit exactly over the other after rigid transformations and dilations.
In this figure, triangle \(ABC\) is similar to triangle \(DEF\).
If \(ABC\) is rotated around point \(B\) and then dilated with center point \(O\), then it will fit exactly over \(DEF\). This means that they are similar.
The slope of a line is a number we can calculate using any two points on the line. To find the slope, divide the vertical distance between the points by the horizontal distance.
The slope of this line is 2 divided by 3 or \(\frac23\).
A solution to an equation with two variables is a pair of values of the variables that make the equation true.
For example, one possible solution to the equation \(4x+3y=24\) is \((6,0)\). Substituting 6 for \(x\) and 0 for \(y\) makes this equation true because \(4(6)+3(0)=24\).
A solution to an inequality is a number that can be used in place of the variable to make the inequality true.
For example, 5 is a solution to the inequality \(c<10\), because it is true that \(5<10\). Some other solutions to this inequality are 9.9, 0, and -4.
A sphere is a three-dimensional figure in which all cross-sections in every direction are circles.
The square root of a positive number \(n\) is the positive number whose square is \(n\). It is also the the side length of a square whose area is \(n\). We write the square root of \(n\) as \(\sqrt{n}\).
For example, the square root of 16, written as \(\sqrt{16}\), is 4 because \(4^2\) is 16.
\(\sqrt{16}\) is also the side length of a square that has an area of 16.
A straight angle is an angle that forms a straight line. It measures 180 degrees.
Supplementary angles have measures that add up to 180 degrees.
For example, a \(15^\circ\) angle and a \(165^\circ\) angle are supplementary.
The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.
For example, if the faces of a cube each have an area of 9 cm2, then the surface area of the cube is \(6 \boldcdot 9\), or 54 cm2.
A system of equations is a set of two or more equations. Each equation contains two or more variables. We want to find values for the variables that make all the equations true.
These equations make up a system of equations:
\(\displaystyle \begin{cases} x + y = \text-2\\x - y = 12\end{cases}\)
The solution to this system is \(x=5\) and \(y=\text-7\) because when these values are substituted for \(x\) and \(y\), each equation is true: \(5+(\text-7)=\text-2\) and \(5-(\text-7)=12\).
A term is a part of an expression. It can be a single number, a variable, or a number and a variable that are multiplied together. For example, the expression \(5x + 18\) has two terms. The first term is \(5x\) and the second term is 18.
A tessellation is a repeating pattern of one or more shapes. The sides of the shapes fit together perfectly and do not overlap. The pattern goes on forever in all directions.
This diagram shows part of a tessellation.
A transformation is a translation, rotation, reflection, or dilation, or a combination of these.
A translation moves every point in a figure a given distance in a given direction.
This diagram shows a translation of Figure A to Figure B using the direction and distance given by the arrow.
A transversal is a line that crosses parallel lines.
This diagram shows a transversal line \(k\) intersecting parallel lines \(m\) and \(\ell\).
A two-way table provides a way to compare two categorical variables.
It shows one of the variables across the top and the other down one side. Each entry in the table is the frequency or relative frequency of the category shown by the column and row headings.
A study investigates the connection between meditation and the state of mind of athletes before a track meet. This two-way table shows the results of the study.
| meditated | did not meditate | total | |
|---|---|---|---|
| calm | 45 | 8 | 53 |
| agitated | 23 | 21 | 44 |
| total | 68 | 29 | 97 |
A vertex is a point where two or more edges meet. When we have more than one vertex, we call them vertices.
The vertices in this polygon are labeled \(A\), \(B\), \(C\), \(D\), and \(E\).
Vertical angles are opposite angles that share the same vertex. They are formed by a pair of intersecting lines. Their angle measures are equal.
For example, angles \(AEC\) and \(DEB\) are vertical angles. If angle \(AEC\) measures \(120^\circ\), then angle \(DEB\) must also measure \(120^\circ\).
Angles \(AED\) and \(BEC\) are another pair of vertical angles.
The vertical intercept is the point where the graph of a line crosses the vertical axis.
The vertical intercept of this line is \((0,\text-6)\) or just -6.
Volume is the number of cubic units that fill a three-dimensional region, without any gaps or overlaps.
For example, the volume of this rectangular prism is 60 units3, because it is composed of 3 layers that are each 20 units3.