If two interior angles lie on opposite sides of the transversal they are called alternate interior angles.
In the figure, \(a\) and \(d\) are alternate interior angles, and \(b\) and \(c\) are also alternate interior angles.
Alternate Interior Angles
Let’s explore why some angles are always equal.
Lines \(AC\) and \(DF\) are parallel. They are cut by transversal \(HJ\).
Description: <p>Line A C contains point B. Line D F contains point E. Line J H contains points B and E. Angle A B J is labeled question mark. Angle A B E is labeled 63 degrees. Angle E B C is labeled question mark. Angle C B J is labeled question mark. Angle D E H is labeled question mark. Angle H E F is labeled question mark. Angle F E B is labeled question mark. Angle B E D is labeled question mark.</p>
With your partner, find the seven unknown angle measures in the diagram. Explain your reasoning.
Using what you noticed, find the measures of the four angles at point \(B\) in the second diagram. Lines \(AC\) and \(DF\) are parallel.
Description: <p>Line A C contains point B. Line D F contains point E. Line H G contains points B and E. Angle A B H is labeled with a question mark. Angle A B E is labeled with a question mark. Angle E B C is labeled with a question mark. Angle C B H is labeled with a question mark. Angle G E F is labeled 34 degrees.</p>
The next diagram resembles the first one, but the lines form slightly different angles. Work with your partner to find the six unknown angles with vertices at points \(B\) and \(E\).
Description: <p>Line A C contains point B. Line D F contains point E. Line J H contains points B and E. Angle A B J is labeled question mark. Angle A B E is labeled 63 degrees. Angle E B C is labeled question mark. Angle C B J is labeled question mark. Angle D E H is labeled question mark. Angle H E F is labeled 108 degrees. Angle F E B is labeled question mark. Angle B E D is labeled question mark.</p>
Description: <p>Four lines on a grid. Line l is a horizontal line 8 units up on the grid. Line m is a horizontal line 3 units up on the grid. A line trends up and to the right and crossed line m at a point between 3 and 4 units to the right and 3 units up. The line crosses line l at a point 7 units to the right and 8 units up. Another line crosses line m at a point between 9 and 10 units to the right and 3 units up. It crosses the line l at a point 7 units to the right and 8 units up. The interior angle at the top of the triangle formed is labeled 60 degrees. The bottom left exterior angle of the bottom left vertex is labeled 55 degrees. The bottom right exterior angle of the bottom right vertex is labeled x degrees.</p>
Parallel lines \(\ell\) and \(m\) are cut by two transversals which intersect \(\ell\) in the same point. Two angles are marked in the figure. Find the measure \(x\) of the third angle.
Lines \(\ell\) and \(k\) are parallel and \(t\) is a transversal. Point \(M\) is the midpoint of segment \(PQ\).
Find a rigid transformation showing that angles \(MPA\) and \(MQB\) are congruent.
Does your argument in the earlier problem apply in this situation? Explain.
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
Silently read your card and think about what information you need to be able to answer the question.
Ask your partner for the specific information that you need.
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
Share the problem card and solve the problem independently.
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
Silently read your card.
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
Read the problem card and solve the problem independently.
Share the data card and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
If two angle measures add up to \(90^\circ\), then we say the angles are complementary. If two angle measures add up to \(180^\circ\), then we say the angles are supplementary. When two lines intersect, vertical angles are equal and adjacent angles are supplementary. For example, in this figure angles 1 and 3 are equal, angles 2 and 4 are equal, angles 1 and 4 are supplementary, and angles 2 and 3 are supplementary.
Description: <p>Two intersecting lines. Angle 1 is labeled 70 degrees. Angle 2 is labeled 110 degrees. Angle 3 is labeled 70 degrees. Angle 4 is labeled 110 degrees.</p>
When two parallel lines are cut by another line, called a transversal, two pairs of alternate interior angles are created. (“Interior” means on the inside, or between, the two parallel lines.) For example, in this figure angles 3 and 5 are alternate interior angles and angles 4 and 6 are also alternate interior angles.
Description: <p>Two lines that do not intersect. A third line intersects with both lines. At the first intersection, angle 1 is labeled 70 degrees. Angle 2 is labeled 110 degrees. Angle 3 is labeled 70 degrees. Angle 4 is labeled 110 degrees. At the second intersection, angle 5 is marked 70 degrees. Angle 6 is marked 110 degrees. Angle 7 is marked 70 degrees. Angle 8 is marked 110 degrees.</p>
Alternate interior angles are equal because a \(180^\circ\) rotation around the midpoint of the segment that joins their vertices takes each angle to the other. Imagine a point \(M\) halfway between the two intersections—can you see how rotating \(180^\circ\) about \(M\) takes angle 3 to angle 5?
Using what we know about vertical angles, adjacent angles, and alternate interior angles, we can find the measures of any of the eight angles created by a transversal if we know just one of them. For example, starting with the fact that angle 1 is \(70^\circ\) we use vertical angles to see that angle 3 is \(70^\circ\), then we use alternate interior angles to see that angle 5 is \(70^\circ\), then we use the fact that angle 5 is supplementary to angle 8 to see that angle 8 is \(110^\circ\) since \(180 -70 = 110\). It turns out that there are only two different measures. In this example, angles 1, 3, 5, and 7 measure \(70^\circ\), and angles 2, 4, 6, and 8 measure \(110^\circ\).
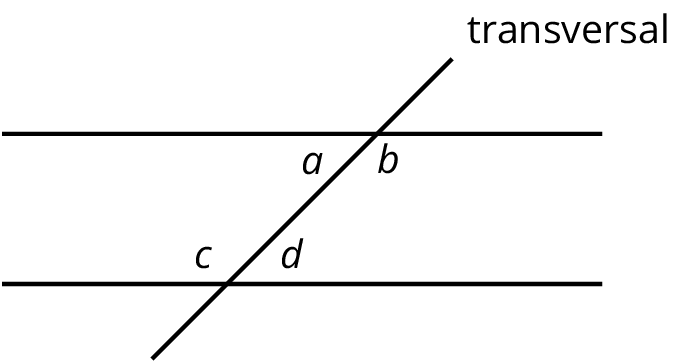
Interior angles are angles that are made by a transversal crossing two parallel lines. They are the angles that lie between the parallel lines, not outside them.
If two interior angles lie on opposite sides of the transversal they are called alternate interior angles.
In the figure, \(a\) and \(d\) are alternate interior angles, and \(b\) and \(c\) are also alternate interior angles.
Complementary angles have measures that add up to 90 degrees.
For example, a \(15^\circ\) angle and a \(75^\circ\) angle are complementary.
Supplementary angles have measures that add up to 180 degrees.
For example, a \(15^\circ\) angle and a \(165^\circ\) angle are supplementary.
A transversal is a line that crosses parallel lines.
This diagram shows a transversal line \(k\) intersecting parallel lines \(m\) and \(\ell\).