If two interior angles lie on opposite sides of the transversal they are called alternate interior angles.
In the figure, \(a\) and \(d\) are alternate interior angles, and \(b\) and \(c\) are also alternate interior angles.
Adding the Angles in a Triangle
Let’s explore angles in triangles.
Share your drawings with a partner. Discuss your thinking. If you disagree, work to reach an agreement.
| acute (all angles acute) | right (has a right angle) | obtuse (has an obtuse angle) | |
|---|---|---|---|
|
scalene (side lengths all different)
|
|||
|
isosceles (at least two side lengthsare equal)
|
|||
|
equilateral (three side lengths equal)
|
Your teacher will give you a card with a picture of a triangle.
The measurement of one of the angles is labeled. Mentally estimate the measures of the other two angles.
Enter the three angle measures for your triangle on the table your teacher has posted.
Your teacher will give you a page with three sets of angles and a blank space. Cut out each set of three angles. Can you make a triangle from each set that has these same three angles?
Draw a quadrilateral. Cut it out, tear off its angles, and line them up. What do you notice?
A \(180^\circ\) angle is called a straight angle because when it is made with two rays, they point in opposite directions and form a straight line.
If we experiment with angles in a triangle, we find that the sum of the measures of the three angles in each triangle is \(180^\circ\)—the same as a straight angle!
Through experimentation we find:
If we add the three angles of a triangle physically by cutting them off and lining up the vertices and sides, then the three angles form a straight angle.
If we have a line and two rays that form three angles added to make a straight angle, then there is a triangle with these three angles.
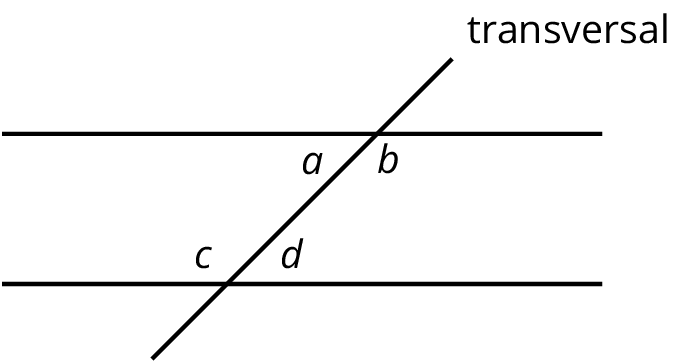
Interior angles are angles that are made by a transversal crossing two parallel lines. They are the angles that lie between the parallel lines, not outside them.
If two interior angles lie on opposite sides of the transversal they are called alternate interior angles.
In the figure, \(a\) and \(d\) are alternate interior angles, and \(b\) and \(c\) are also alternate interior angles.
Complementary angles have measures that add up to 90 degrees.
For example, a \(15^\circ\) angle and a \(75^\circ\) angle are complementary.
A straight angle is an angle that forms a straight line. It measures 180 degrees.
Supplementary angles have measures that add up to 180 degrees.
For example, a \(15^\circ\) angle and a \(165^\circ\) angle are supplementary.
A transversal is a line that crosses parallel lines.
This diagram shows a transversal line \(k\) intersecting parallel lines \(m\) and \(\ell\).