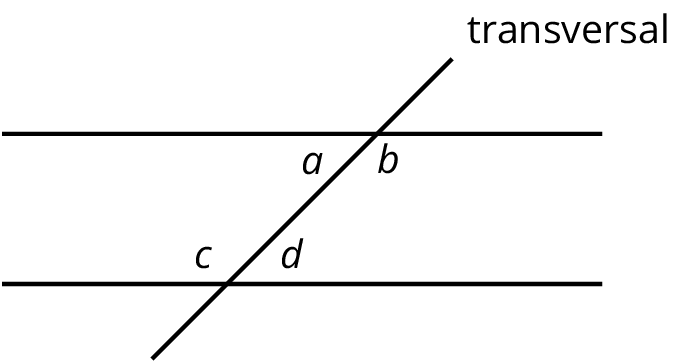
If two interior angles lie on opposite sides of the transversal they are called alternate interior angles.
In the figure, \(a\) and \(d\) are alternate interior angles, and \(b\) and \(c\) are also alternate interior angles.
Alternate Interior Angles
In this lesson, students justify that alternate interior angles are congruent, and use this and the vertical angle theorem, previously justified, to solve problems. They are also introduced to the terms complementary, for describing two angles whose measures add to \(90^\circ\), and supplementary, for describing two angles whose measures add to \(180^\circ\). They practice finding an unknown angle given the measure of another angle that is complementary or supplementary.
Thus far in this unit, students have studied different types of rigid motions, using them to examine and build different figures. This work continues here, with an emphasis on examining angles. In a previous lesson, \(180^\circ\) rotations were employed to show that vertical angles, made by intersecting lines, are congruent. The warm-up recalls previous facts about angles made by intersecting lines, including both vertical and adjacent angles. Next a third line is added, parallel to one of the two intersecting lines. There are now 8 angles, 4 each at the 2 intersection points of the lines. At each vertex, vertical and adjacent angles can be used to calculate all angle measures once one angle is known. But how do the angle measures compare at the two vertices? It turns out that each angle at one vertex is congruent to the corresponding angle (via translation) at the other vertex and this can be seen using rigid motions: translations and \(180^\circ\) rotations are particularly effective at revealing the relationships between the angle measures.
During the lesson, students will notice as they calculate angles that they are repeatedly using vertical and adjacent angles and that often they have a choice which method to apply (MP8). They will also notice that the angles made by parallel lines cut by a transversal are the same and this observation is the key structure in this lesson.
This lesson is the first time students see the terms complementary and supplementary angles in IM 6–8 Math Accelerated. Make sure to highlight their use during the lesson synthesis in addition to the focus on alternate interior angles. Here are some possible questions to include in the discussion:
Teacher Facing
Let’s explore why some angles are always equal.
Students need rulers and tracing paper from the geometry toolkits.
Interior angles are angles that are made by a transversal crossing two parallel lines. They are the angles that lie between the parallel lines, not outside them.
If two interior angles lie on opposite sides of the transversal they are called alternate interior angles.
In the figure, \(a\) and \(d\) are alternate interior angles, and \(b\) and \(c\) are also alternate interior angles.
Complementary angles have measures that add up to 90 degrees.
For example, a \(15^\circ\) angle and a \(75^\circ\) angle are complementary.
Supplementary angles have measures that add up to 180 degrees.
For example, a \(15^\circ\) angle and a \(165^\circ\) angle are supplementary.
A transversal is a line that crosses parallel lines.
This diagram shows a transversal line \(k\) intersecting parallel lines \(m\) and \(\ell\).
Teachers with a valid work email address can click here to register or sign in for free access to Cool Down, Teacher Guide, and PowerPoint materials.
| Student Task Statements | docx | |
| Cumulative Practice Problem Set | docx | |
| Cool Down | Log In | |
| Teacher Guide | Log In | |
| Teacher Presentation Materials | docx | |
| Blackline Masters | zip |