Lección 16

Dos cantidades relacionadas (Parte 1)

Usemos ecuaciones y gráficas para describir relaciones dadas por razones.

16.1: ¿Cuál escogerías?

¿Cuál escogerías? Prepárate para explicar tu razonamiento.

  • Una jarra de 5 libras de miel por \$15.35
  • Tres jarras de 1.5 libras de miel por \$13.05

 

16.2: Pintar el set

Lin necesita mezclar un tono específico de pintura naranja para el set de la obra de teatro escolar. El color utiliza 3 partes de amarillo por cada 2 partes de rojo.

  1. Completa la tabla que muestra diferentes combinaciones de pintura roja y amarilla que producirán el tono de anaranjado que Lin necesita.

    tazas de pintura roja \((r)\) tazas de pintura amarilla \((y)\) total de tazas de pintura \((t)\)
    2 3  
    6    
        20
      18  
    14    
    16    
        50
      42  
  2. Lin observa que el número de tazas de pintura roja siempre es \(\frac25\) del total de tazas de pintura. Ella escribe la ecuación \(r=\frac25 t\) para describir la relación. ¿Cuál es la variable independiente? ¿Cuál es la variable dependiente? Explica cómo lo sabes.
  3. Escribe una ecuación que describa la relación entre \(r\) y \(y\) en la que \(y\) sea la variable independiente.
  4. Escribe una ecuación que describa la relación entre \(y\) y \(r\) en la que \(r\) sea la variable independiente.
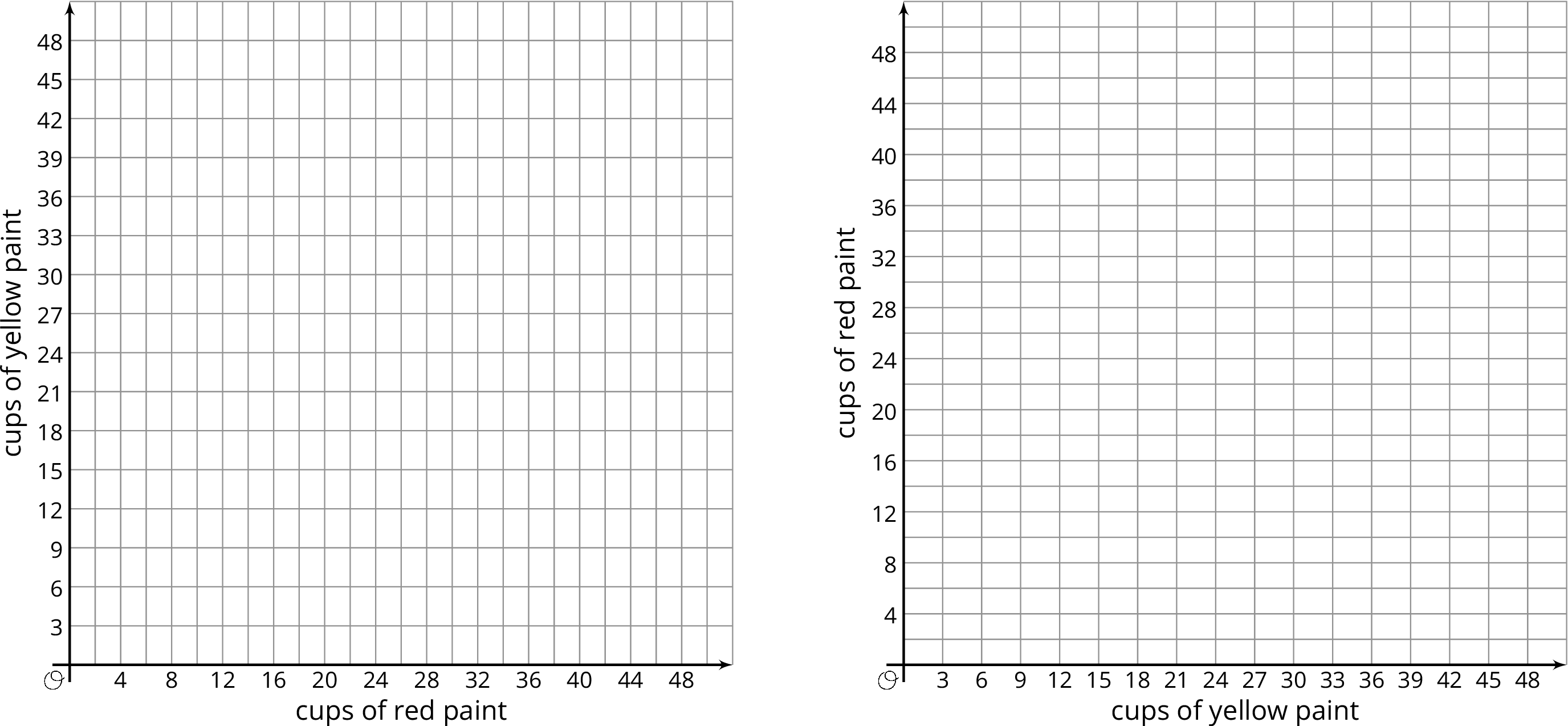
  5. Utiliza los puntos de la tabla para crear dos gráficas que muestren la relación entre \(r\) y \(y\). Empareja cada relación con una de las ecuaciones que escribiste.
Two blank coordinate planes with origins labeled "O". For the coordinate plane on the left: the horizontal axis is labeled “cups of red paint” and the numbers 0 through 48, in increments of 4, are indicated. There are gridlines midway between each number. The vertical axis is labeled “cups of yellow paint” and the numbers 0 through 48, in increments of 3, are indicated. For the coordinate plane on the right: the horizontal axis is labeled “cups of yellow paint” and the numbers 0 through 48, in increments of 3, are indicated. The vertical axis is labeled “cups of red paint” and the numbers 0 through 48, in increments of 4, are indicated. There are gridlines midway between each number.


En un puesto de frutas venden manzanas, duraznos y tomates. Hoy vendieron 4 manzanas por cada 5 duraznos. Vendieron 2 duraznos por cada 3 tomates. En total vendieron 132 frutas. ¿Cuántas unidades vendieron de cada fruta? 

Resumen

Las ecuaciones son muy útiles para describir conjuntos de razones equivalentes. Este es un ejemplo de eso:

Una receta de una tarta requiere 3 manzanas verdes por cada 5 manzanas rojas. Podemos crear una tabla para mostrar algunas razones equivalentes.

manzanas verdes (g) manzanas rojas (r)
3 5
6 10
9 15
12 20

Podemos ver de la tabla que \(r\) siempre es \(\frac53\) tan grande como \(g\) y que \(g\) siempre es \(\frac35\) tan grande como \(r\). Podemos escribir ecuaciones para describir la relación entre \(g\) y \(r\).

  • Cuando conocemos el número de manzanas verdes y queremos hallar el número de manzanas rojas, podemos escribir: \(\displaystyle r=\frac53g\) En esta ecuación, si \(g\) cambia, \(r\) es afectada por el cambio, así que nos referimos a \(g\) como la variable independiente y a \(r\) como la variable dependiente.

    Podemos utilizar esta ecuación con cualquier valor de \(g\) para hallar \(r\). Si se utilizan 270 manzanas verdes, entonces se utilizan \(\frac53 \boldcdot (270)\) o 450 manzanas rojas.

  • Cuando conocemos el número de manzanas rojas y queremos hallar el número de manzanas verdes, podemos escribir: \(\displaystyle g=\frac35r\) En esta ecuación, si \(r\) cambia, \(g\) es afectada por el cambio, así que nos referimos a \(r\) como la variable independiente y a \(g\) como la variable dependiente.

    Podemos utilizar esta ecuación con cualquier valor de \(r\) para hallar \(g\). Si se utilizan 275 manzanas rojas, entonces se utilizan \(\frac35 \boldcdot (275)\) o 165 manzanas verdes.

También podemos graficar las dos ecuaciones que escribimos para obtener una representación visual de la relación entre las dos cantidades.

Entradas del glosario

  • variable dependiente

    La variable dependiente es el resultado de un cálculo. Por ejemplo, un barco viaja a una rapidez constante de 25 millas por hora. La ecuación \(d=25t\) describe la relación entre la distancia recorrida por el bote y el tiempo transcurrido. La variable dependiente es la distancia recorrida porque \(d\) es el resultado de multiplicar 25 por \(t\).

  • variable independiente

    La variable independiente se usa para calcular el valor de otra variable. Por ejemplo, un barco viaja a una rapidez constante de 25 millas por hora. La ecuación \(d=25t\) describe la relación entre la distancia recorrida por el bote y el tiempo transcurrido. La variable independiente es el tiempo transcurrido porque \(t\) es multiplicado por 25 para obtener \(d\).