Lección 18
Más relaciones
Utilicemos gráficas y ecuaciones para mostrar relaciones que involucren área, volumen y exponentes.
18.1: Cuál es diferente: gráficas
18.2: Hacer un cartel
Mai va a elaborar un cartel rectangular para promocionar la obra de teatro escolar. El material requerido para el cartel se vende por pie cuadrado. Mai tiene dinero suficiente para comprar 36 pies cuadrados de material. Ella está tratando de decidir qué largo y qué ancho tendrá el cartel.
- Si el largo es 6 pies, ¿cuál es el ancho?
- Si el largo es 4 pies, ¿cuál es el ancho?
- Si el largo es 9 pies, ¿cuál es el ancho?
- Para hallar diferentes combinaciones de largo y ancho que den un área de 36 pies cuadrados, Mai utiliza la ecuación \(w=\frac{36}{\ell}\), donde \(w\) es el ancho y \(\ell\) es el largo. Compara tu estrategia con el método de Mai para hallar el ancho. ¿En qué se parecen o se diferencian?
-
Utiliza varias combinaciones de largo y ancho para crear una gráfica que muestre la relación entre las longitudes de lado de varios rectángulos que tengan un área de 36 pies cuadrados.

- Explica cómo describe la gráfica la relación que hay entre el largo y el ancho para diferentes rectángulos que tienen un área de 36.
- Supongamos que Mai utilizó la ecuación \(\ell=\frac{36}{w}\) para hallar los largos para diferentes valores del ancho. ¿La gráfica sería diferente si ella graficara el largo en el eje vertical y el ancho en el eje horizontal? Explica cómo lo sabes.
18.3: Cajas de cereal
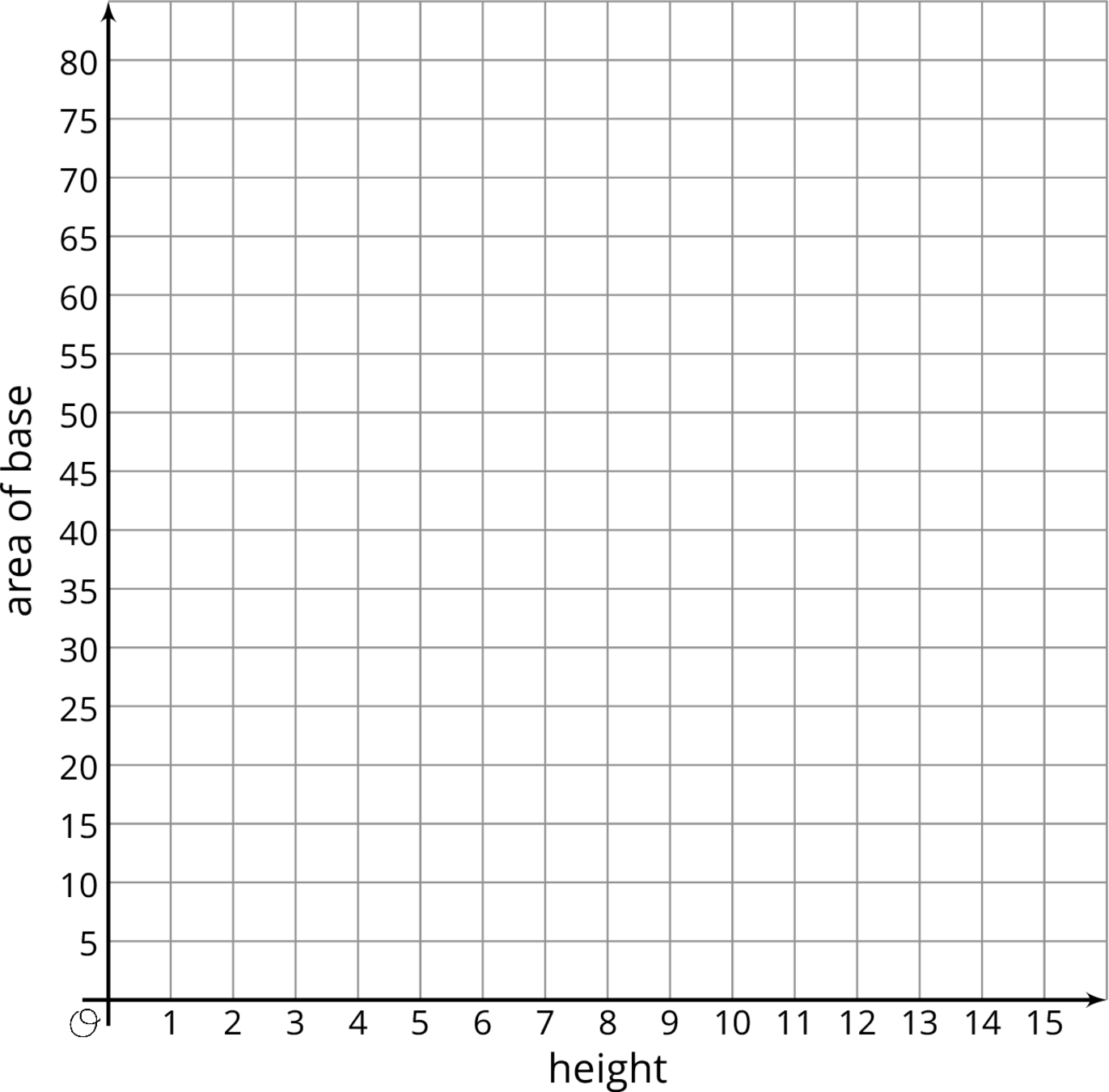
Un productor de cereal necesita diseñar una caja de cereal que tenga un volumen de 225 pulgadas cúbicas y una altura que no sea mayor a 15 pulgadas.
- Los diseñadores saben que el volumen de un prisma rectangular se puede calcular multiplicando el área de su base y su altura. Completa la tabla con pares de valores que hagan que el volumen sea 225 in3.
altura (in) 5 9 12 7\(\frac12\) área de la base (in2) 75 15 - Describe cómo hallaste los valores que hacían falta en la tabla.
- Escribe una ecuación que muestre cómo el área de la base, \(A\), es afectada por los cambios en la altura, \(h\), para diferentes prismas rectangulares que tengan un volumen de 225 in3.
-
Dibuja los pares ordenados de la tabla en la gráfica para mostrar la relación que hay entre el área de la base y la altura para diferentes cajas que tengan un volumen de 225 in3.
18.4: Los mosquitos se multiplican
Un investigador que estudia poblaciones de mosquitos recolecta los siguientes datos:
| día del estudio \((d)\) |
número de mosquitos \((n)\) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
-
El investigador dijo que, para estos cinco días, el número de mosquitos, \(n\), se puede hallar por medio de la ecuación \(n = 2^d\), donde \(d\) es el número de día del estudio. Explica por qué esta ecuación concuerda con los datos.
-
Utiliza los pares ordenados en la tabla para graficar la relación que hay entre el número de mosquitos y el día del estudio para estos cinco días.
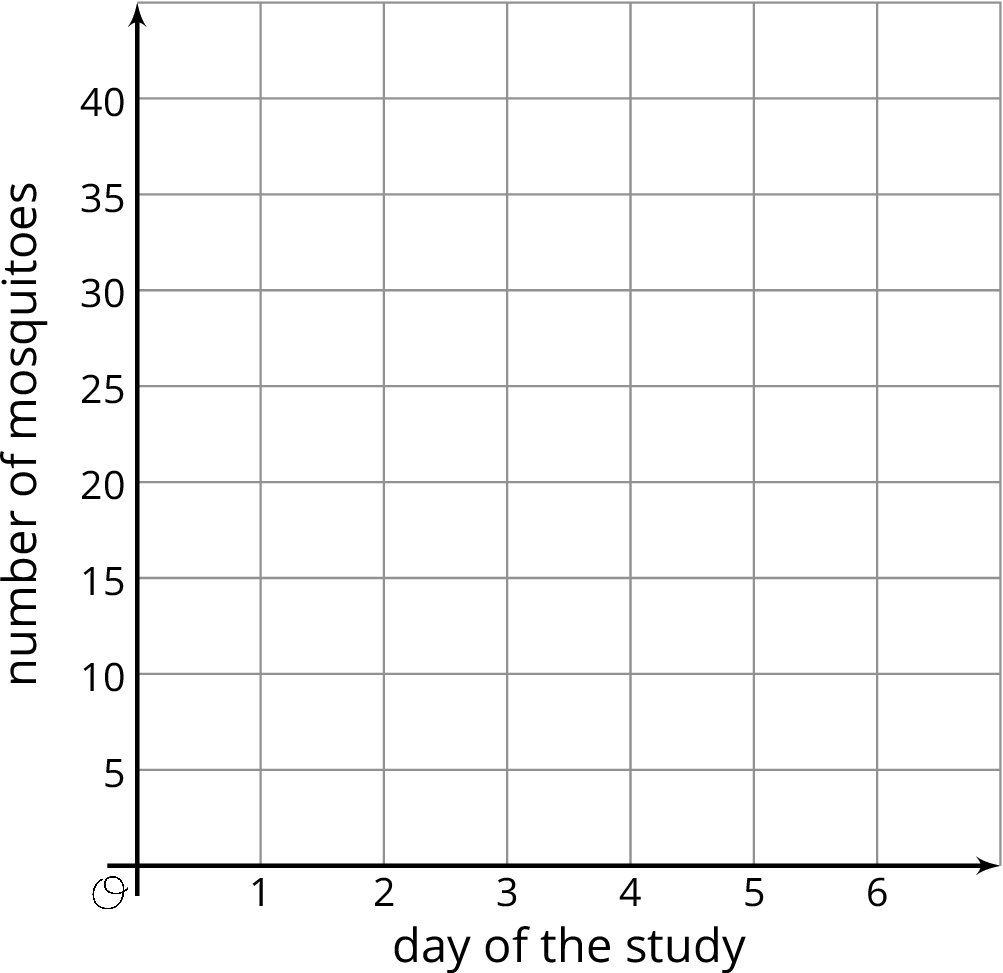
- Describe la gráfica. Compara cómo los datos, la ecuación y la gráfica ilustran la relación que hay entre el día del estudio y el número de mosquitos.
-
Si el patrón continúa, ¿cuántos mosquitos habrá el día 6?
Resumen
Las ecuaciones pueden representar relaciones entre cantidades geométricas. Por ejemplo:
- Si \(s\) representa la longitud de lado de un cuadrado, entonces el área \(A\) está relacionada con \(s\) \(A = s^2\)
- A veces las relaciones son más específicas. Por ejemplo, el perímetro \(P\) de un rectángulo que tiene largo \(l\) y ancho \(w\) es \(P=2l+2w\). Si solo consideramos rectángulos que tengan largo 10, entonces la relación entre el perímetro y el ancho es \(P = 20 + 2w\)
Este es otro ejemplo de una ecuación con un exponente que expresa la relación entre cantidades:
-
Una pelota de caucho se deja caer desde una altura de 10 pies. En cada rebote consecutivo la pelota solo alcanza \(\frac{1}{2}\) de la altura del rebote anterior.
Esto significa que en el primer rebote la pelota rebotará hasta 5 pies de altura y luego, en el segundo rebote, solo alcanzará \(2\frac{1}{2}\) pies de altura, y así sucesivamente. Podemos representar esta situación con una ecuación para hallar qué tan alto rebotará la pelota después de cualquier número de rebotes.
Para hallar qué tan alto rebota la pelota en el \(n\)-ésimo rebote, debemos multiplicar 10 pies (la altura inicial) por \(\frac{1}{2}\) y multiplicar nuevamente por \(\frac{1}{2}\) por cada rebote a partir de ese; debemos hacer esto \(n\) veces. Entonces la altura, \(h\), de la pelota en el \(n\)-ésimo rebote será \(h =10\left(\frac{1}{2}\right)^n\). En esta ecuación, la variable dependiente, \(h\), es afectada por los cambios en la variable independiente, \(n\).
Las ecuaciones y las gráficas pueden darnos intuición en diferentes tipos de relaciones entre cantidades y ayudarnos a responder preguntas y a resolver problemas.
Entradas del glosario
- plano de coordenadas
El plano de coordenadas es un sistema para especificar la ubicación de puntos. Por ejemplo, el punto \(R\) está ubicado en \((3, 2)\) en el plano de coordenadas, porque está tres unidades a la derecha y dos unidades arriba del origen.
- variable dependiente
La variable dependiente es el resultado de un cálculo. Por ejemplo, un barco viaja a una rapidez constante de 25 millas por hora. La ecuación \(d=25t\) describe la relación entre la distancia recorrida por el bote y el tiempo transcurrido. La variable dependiente es la distancia recorrida porque \(d\) es el resultado de multiplicar 25 por \(t\).
- variable independiente
La variable independiente se usa para calcular el valor de otra variable. Por ejemplo, un barco viaja a una rapidez constante de 25 millas por hora. La ecuación \(d=25t\) describe la relación entre la distancia recorrida por el bote y el tiempo transcurrido. La variable independiente es el tiempo transcurrido porque \(t\) es multiplicado por 25 para obtener \(d\).