Lección 5

Este diagrama de puntos muestra los pesos de las mochilas, en kilogramos, de 50 estudiantes de sexto grado en una escuela en Nueva Zelanda. 

1. El diagrama de puntos muestra varios puntos en 0 kilogramos. ¿Qué podría significar un valor de 0 en este contexto?

2. Clare y Tyler analizaron el diagrama de puntos.

   • Clare dijo: "Yo creo que podemos utilizar 3 kilogramos para describir un peso de mochila típico para el grupo porque representa el 20% (o la mayor porción) de los datos".

   • Tyler no estuvo de acuerdo y dijo: "Yo creo que 3 kilogramos es muy poco para describir un peso típico. La mitad de los puntos representan mochilas que pesan más de 3 kilogramos, así que yo utilizaría un valor mayor". 

   ¿Estás de acuerdo con alguno de ellos? Explica tu razonamiento.

Se pidió a veinticinco estudiantes de sexto grado que estimaran cuántas horas por cada semana dedican a hablar por teléfono. Este diagrama de puntos representa el número de horas por cada semana reportadas de uso de teléfono.

1. 1. ¿Cuántos estudiantes reportaron que no hablan por teléfono durante la semana? Explica cómo lo sabes.
   2. ¿Qué porcentaje de estudiantes reportaron que no hablan por teléfono?
2. 1. ¿Cuál es el mayor número de horas que un estudiante dedica a hablar por teléfono por cada semana?
   2. ¿Qué porcentaje del grupo reportó hablar por teléfono esta cantidad de tiempo?
3. 1. ¿Cuántas horas dirías que estos estudiantes dedican típicamente a hablar por teléfono?
   2. ¿Cuántos minutos al día sería eso?
4. 1. ¿Cómo describirías la dispersión de los datos? ¿Consideras que las cantidades de tiempo que estos estudiantes pasan en el teléfono son parecidas o diferentes? Explica tu razonamiento.
   2. Este es el diagrama de puntos de una actividad anterior. En el diagrama podemos ver el número de horas por cada semana que el mismo grupo de 25 estudiantes de sexto grado reportó que dedica en la casa a hacer tareas.
      

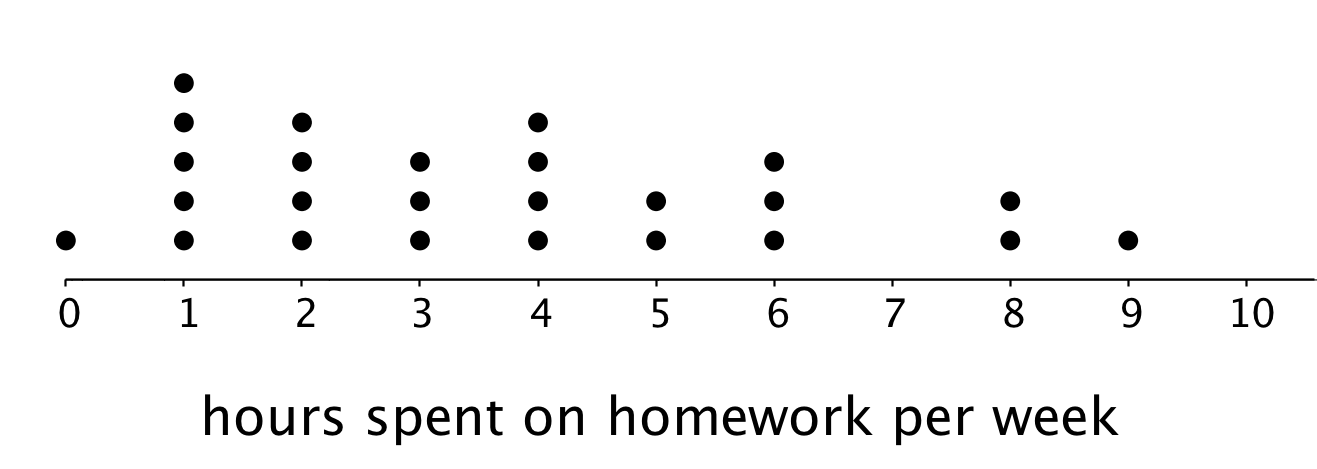
      En general, ¿estos estudiantes se parecen más en el tiempo que dedican a hablar por teléfono o en el tiempo que dedican a hacer tareas? Explica tu razonamiento.

5. Supongamos que alguien afirmó que estos estudiantes de sexto grado dedican mucho tiempo a hablar por teléfono. ¿Estás de acuerdo? Utiliza tu análisis del diagrama de puntos para apoyar tu respuesta.

1. Una profesora de mecanografía se preguntó: "¿La rapidez de los estudiantes al teclear aumenta después de tomar un curso de mecanografía?". Explica por qué su pregunta es una pregunta estadística.
2. La profesora registró el número de palabras que sus estudiantes podían teclear por cada minuto al inicio del curso y nuevamente al finalizarlo. Los dos diagramas de puntos muestran los dos conjuntos de datos.

   

   

   Basándote en los diagramas de puntos, ¿con cuáles de las siguientes afirmaciones sobre el grupo de estudiantes estás de acuerdo? Prepárate para explicar tu razonamiento.

   1. En general, la rapidez de los estudiantes al teclear no aumentó. Ellos teclean con la misma rapidez al finalizar el curso que como lo hacían al inicio.

   2. 20 palabras por minuto es una buena estimación para qué tan rápido, en general, tecleaban los estudiantes al inicio del curso. 

   3. 20 palabras por minuto es una buena descripción del centro del conjunto de datos al finalizar el curso.

   4. Hay más variabilidad en las rapideces al teclear en el inicio del curso que al final, así que las rapideces de los estudiantes al teclear fueron más parecidas al finalizarlo. 

3. En general, ¿qué tan rápido dirías que los estudiantes teclean después de completar el curso? ¿Cuál consideras que es el centro de los datos del final del curso?

Una forma de describir lo que es típico o característico en un conjunto de datos es mirar el centro y la dispersión de su distribución.

Comparemos las distribuciones de los pesos de los gatos y los pesos de los perros que se muestran en estos diagramas de puntos. 

La colección de puntos que representan los datos sobre los gatos está más hacia la izquierda de la recta numérica que la de los puntos que representan los datos sobre los perros. Basados en los diagramas de puntos, podemos decir que el centro de la distribución para los pesos de los gatos está entre 4 y 5 kilogramos y que el centro para los pesos de los perros está entre 7 y 8 kilogramos.

A menudo decimos que los valores que están en el centro de una distribución o cerca de este son típicos para ese grupo. Esto significa que un peso de 4 o 5 kilogramos es típico para un gato del conjunto de datos y un peso de 7 u 8 kilogramos es típico para un perro.

También vemos que los pesos de los perros están más dispersos que los pesos de los gatos. La diferencia entre el gato más pesado y el más liviano es tan solo 4 kilogramos, mientras que la diferencia entre el perro más pesado y el más liviano es 6 kilogramos.

Una distribución que tiene una mayor dispersión nos dice que los datos tienen mayor variabilidad. En este caso, podemos decir que los gatos se parecen más en sus pesos que los perros.

En lecciones futuras vamos a discutir cómo medir el centro y la dispersión de una distribución.