Lección 5

Movidas con coordenadas

Transformemos algunas figuras y veamos qué le pasa a las coordenadas de los puntos. 

5.1: Traslademos coordenadas

Elige todas las traslaciones que lleven al triángulo T hasta el triángulo U. Puede que haya más de una respuesta correcta.

Two triangles on a coordinate grid. Triangle U has vertices (1, 2), (2,1), (0, -1). Triangle T has vertices (-3,0), (-2,-1), (-4, -3)
  1. Trasladar \((\text-3,0)\) a \((1,2)\).
  2. Trasladar \((2,1)\) a \((\text-2,\text-1)\).
  3. Trasladar \((\text-4,\text-3)\) a \((0,\text-1)\).
  4. Trasladar \((1,2)\) a \((2,1)\).

5.2: Reflexiones de puntos en el plano de coordenadas

A coordinate grid. The x axis runs from -10 to 10. The y axis runs from -8 to 8.

  1. Esta es una lista de puntos \(\displaystyle \begin{align*}  A&= (0.5,4) & B& = (\text-4,5) & C&=(7,\text-2) & D& = (6,0) & E&= (0,\text-3)\\ & \end{align*}\) Sobre el plano de coordenadas:

    1. Ubica cada punto y etiquétalo con sus coordenadas.
    2. Usando el eje \(x\) como recta de reflexión, ubica la imagen de cada punto.
    3. Etiqueta la imagen de cada punto con sus coordenadas.
    4. Incluye una etiqueta que contenga una letra. Por ejemplo, la imagen del punto \(A\) se debería llamar \(A’\).

  2. Si el punto \((13,10)\) se reflejara usando el eje \(x\) como recta de reflexión, ¿cuáles serían las coordenadas de la imagen?, ¿y para \((13, \text-20)\)? ¿\((13, 570)\)? Explica cómo lo sabes.

  3. El punto \(R\) tiene coordenadas \((3,2)\).

    1. Sin graficar, predice las coordenadas de la imagen del punto \(R\) si el punto \(R\) se reflejara usando el eje \(y\) como recta de reflexión.
    2. Verifica tu respuesta encontrando la imagen de \(R\) sobre la gráfica.
      Point \(R\) on a coordinate plane, origin \(O\). Horizontal and vertical axis scale negative 4 to 4 by 1’s. The point has coordinates \(R\)(3 comma 2).
    3. Etiqueta la imagen del punto \(R\) con \(R’\).

    4. ¿Cuáles son las coordenadas de \(R’\)?

  4. Supongamos que reflejas un punto usando el eje \(y\) como recta de reflexión. ¿Cómo describirías su imagen?

5.3: Transformaciones de un segmento

Segment \(\overline{ A B }\) on a coordinate plane, origin \(O\). Horizontal axis scale negative 5 to 9 by 1’s. Vertical axis scale negative 4 to 8 by 1’s. The coordinates of \(\overline{ AB }\) are \(A\)(0 comma 3) and \(B\)(4 comma 2).

Realiza cada una de las siguientes transformaciones al segmento \(AB\).

  1. Rota el segmento \(AB\) 90 grados en el sentido contrario a las manecillas del reloj alrededor del centro \(B\). Etiqueta la imagen de \(A\) con \(C\). ¿Cuáles son las coordenadas de \(C\)?

  2. Rota el segmento \(AB\) 90 grados en el sentido contrario a las manecillas del reloj alrededor del centro \(A\). Etiqueta la imagen de \(B\) con \(D\). ¿Cuáles son las coordenadas de \(D\)?

  3. Rota el segmento \(AB\) 90 grados en el sentido de las manecillas del reloj alrededor de \((0,0)\). Etiqueta la imagen de \(A\) con \(E\) y la imagen de \(B\) con \(F\). ¿Cuáles son las coordenadas de \(E\) y de \(F\)?

  4. Compara las dos rotaciones de 90 grados en el sentido contrario a las manecillas del reloj del segmento \(AB\). ¿Qué tienen en común las imágenes de estas rotaciones?, ¿en qué se diferencian?



Supongamos que \(EF\) y \(GH\) son segmentos de recta de la misma longitud. Describe una secuencia de transformaciones que lleve \(EF\) hasta \(GH\).

Resumen

Podemos usar coordenadas para describir puntos y encontrar patrones en las coordenadas de los puntos transformados.

Quadrilateral on a coordinate plane.

Podemos describir una traslación expresándola como una secuencia de traslaciones verticales y horizontales. Por ejemplo, el segmento \(AB\) se traslada 3 hacia la derecha y 2 hacia abajo. 

Al reflejar un punto con respecto a un eje se cambia el signo de una coordenada. Por ejemplo, al reflejar el punto \(A\) cuyas coordenadas son \((2,\text-1)\) con respecto al eje \(x\) se cambia el signo de la coordenada \(y\), de forma que su imagen es el punto \(A'\) cuyas coordenadas son \((2,1)\). Al reflejar el punto \(A\) con respecto al eje \(y\) se cambia el signo de la coordenada \(x\), de forma que su imagen es el punto \(A''\) cuyas coordenadas son \((\text-2,\text-1)\).

3 points on a coordinate plane.


Las reflexiones con respecto a otras rectas son más complicadas de describir. 

Segment A B rotated on a coordinate plane, origin O.

Aún no tenemos las herramientas para describir las rotaciones en términos de coordenadas en general. Este es un ejemplo de una rotación de \(90^\circ\) con centro en \((0,0)\) en el sentido contrario a las manecillas del reloj.

El punto \(A\) tiene coordenadas \((0,0)\). El segmento \(AB\) se rotó \(90^\circ\) en el sentido contrario a las manecillas del reloj alrededor de \(A\). El punto \(B\) de coordenadas \((2,3)\) se rota hasta el punto \(B'\) cuyas coordenadas son \((\text-3,2)\).

Entradas del glosario

  • en el sentido contrario a las manecillas del reloj

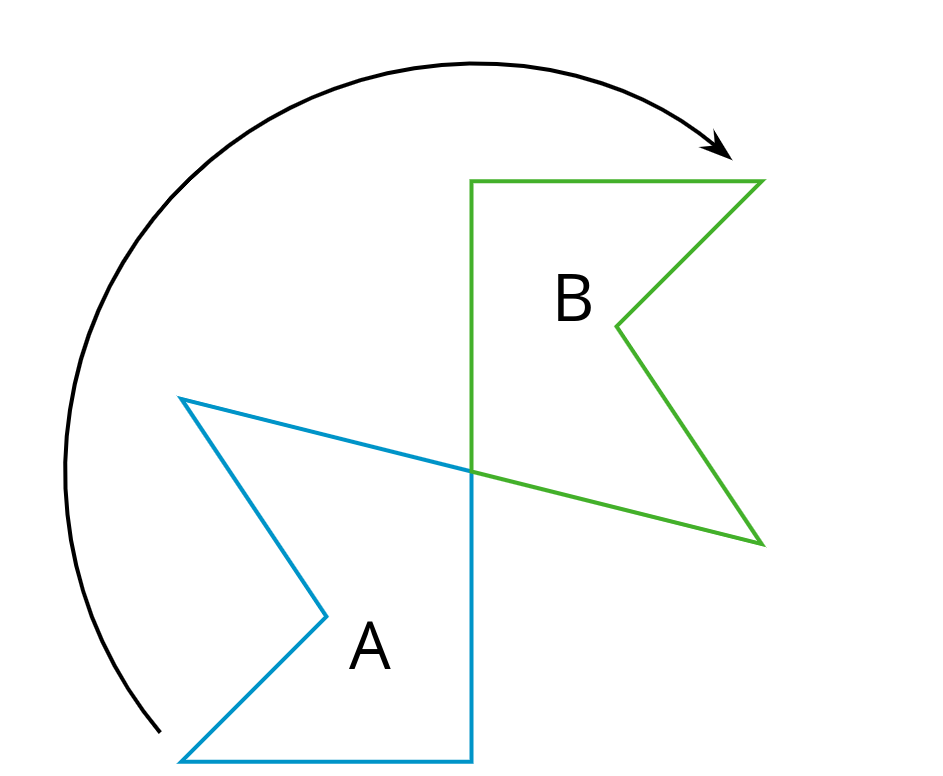
    En el sentido contrario a las manecillas del reloj significa que se gira en la dirección opuesta a la dirección en la cual giran las manecillas de un reloj. Así, un punto que está encima del centro de rotación gira hacia la izquierda.

    Este diagrama muestra como la figura A gira en el sentido contrario a las manecillas del reloj para formar a la figura B.

    Two figures. Figure A turned counterclockwise makes Figure B.
  • en el sentido de las manecillas del reloj

    En el sentido de las manecillas del reloj significa que se gira en la misma dirección que giran las manecillas de un reloj. Así, un punto que está encima del centro de rotación gira hacia la derecha. Este diagrama muestra como la figura A se giró en el sentido de las manecillas del reloj para formar la figura B.

  • imagen

    Una imagen es el resultado de aplicar traslaciones, rotaciones y reflexiones a un objeto. Cada parte del objeto original se mueve de la misma manera para coincidir con la parte correspondiente de la imagen.

    En este diagrama, el triángulo \(ABC\) fue trasladado hacia arriba y hacia la derecha para forma el triángulo \(DEF\). El triángulo \(DEF\) es la imagen del triángulo original \(ABC\).

    2 triangles, ABC and DEF. Triangle ABC has been translated up and to the right to make triangle DEF. Triangle DEF is the image of the original triangle ABC.
  • plano de coordenadas

    El plano de coordenadas es un sistema para especificar la ubicación de puntos. Por ejemplo, el punto \(R\) está ubicado en \((3, 2)\) en el plano de coordenadas, porque está tres unidades a la derecha y dos unidades arriba del origen.

    Point \(R\) on a coordinate plane, origin \(O\). Horizontal and vertical axis scale negative 4 to 4 by 1’s. The point has coordinates \(R\)(3 comma 2).
  • reflexión

    Una reflexión con respecto a una recta toma cada punto de una figura y lo mueve de manera perpendicular a un punto que está ubicado al lado opuesto de esa recta. El nuevo punto está a la misma distancia de la recta que el punto original.

    Este diagrama muestra una reflexión de A con respecto a la recta \(\ell\) que produce la figura imagen B.

    Two triangles, A and B. A reflection of A over a line makes the mirror image B.
  • rotación

    Una rotación hace girar cada punto de una figura alrededor de un centro con un ángulo dado en una dirección específica.

    Este diagrama muestra como al rotar el triángulo A alrededor del centro \(O\) con un ángulo de 55 grados en la dirección de las manecillas del reloj, se obtiene el triángulo B.

    Two trianges, A and B. Triangle A rotated by 55 degrees clockwise gets Triangle B.
  • secuencia de transformaciones

    Una secuencia de transformaciones es un conjunto de traslaciones, rotaciones, reflexiones y dilataciones de una figura, que se realizan en un orden dado.

    Este diagrama muestra una secuencia de transformaciones que lleva la figura A a la figura C.

    Primero, A se traslada hacia la derecha para formar B. Luego, B se refleja con respecto a la recta \(\ell\) para formar C.

    Transformation taking figure A to figure B.
  • transformación

    Una transformación es una traslación, una rotación, una reflexión, una dilatación o una combinación de ellas.

  • traslación

    Una traslación mueve cada punto de una figura cierta distancia en cierta dirección.

    Este diagrama muestra cómo la figura A se traslada para obtener la figura B usando la dirección y la distancia indicadas por la flecha.

    A translation of triangle A to triangle B
  • vértice

    Un vértice es un punto en donde dos o más aristas se encuentran. Los vértices de este polígono están etiquetados con las letras \(A\), \(B\), \(C\), \(D\) y \(E\).

    Polygon with 5 sides