Lección 3
Movidas en la cuadrícula
Transformemos algunas figuras en las cuadrículas.
3.1: Observa y pregúntate: la cuadrícula isométrica
¿Qué observas? ¿Qué te preguntas?
3.2: Información de transformación
Tu profesor te dará papel de calcar para hacer las movidas especificadas. Usa \(A'\), \(B'\), \(C'\) y \(D'\) para indicar los vértices de la nueva figura que corresponden a los puntos \(A\), \(B\), \(C\) y \(D\) en la figura original.
-
En la figura, 1 traslada el triángulo \(ABC\) de forma que \(A\) vaya a \(A'\).
-
En la figura 2, traslada el triángulo \(ABC\) de forma que \(C\) vaya a \(C'\).
-
En la figura 3, rota el triángulo \(ABC\) \(90^\circ\) en el sentido contrario a las manecillas del reloj usando el centro \(O\).
-
En la figura 4, refleja el triángulo \(ABC\) usando la recta \(\ell\).
-
En la figura 5, rota el cuadrilátero \(ABCD\) \(60^\circ\) en el sentido contrario a las manecillas del reloj usando el centro \(B\).
-
En la figura 6, rota el cuadrilátero \(ABCD\) \(60^\circ\) en el sentido de las manecillas del reloj usando el centro \(C\).
-
En la figura 7, refleja el cuadrilátero \(ABCD\) usando la recta \(\ell\).
-
En la figura 8, traslada el cuadrilátero \(ABCD\) de forma que \(A\) vaya a \(C\).
El efecto de cada movida se puede deshacer usando otra movida. Por ejemplo, para deshacer el efecto de trasladar 3 unidades hacia la derecha, podríamos trasladar 3 unidades hacia la izquierda. ¿Qué movida deshace cada una de las siguientes movidas?
- Trasladar 3 unidades hacia arriba
- Trasladar 1 unidad hacia arriba y 1 unidad hacia la izquierda
- Rotar 30 grados en el sentido de las manecillas del reloj alrededor de un punto \(P\)
-
Reflejar con respecto a la recta \(\ell\)
Resumen
Cuando una figura está en una cuadrícula, podemos usar la cuadrícula para describir una transformación. Por ejemplo, esta es una figura y una imagen de la figura luego de una movida.
El cuadrilátero \(ABCD\) se traslada 4 unidades a la derecha y 3 unidades hacia abajo, a la posición del cuadrilátero \(A'B'C'D'\).
Un segundo tipo de cuadrícula se llama cuadrícula isométrica. La cuadrícula isométrica está hecha de triángulos equiláteros. Todos los ángulos de los triángulos miden 60 grados, esto hace que la cuadrícula isométrica sea conveniente para mostrar rotaciones de 60 grados.
Este es el cuadrilátero \(KLMN\) y esta es su imagen \(K'L'M'N'\) luego de una rotación de 60 grados en el sentido contrario a las manecillas del reloj alrededor de un punto \(P\).
Entradas del glosario
- en el sentido contrario a las manecillas del reloj
En el sentido contrario a las manecillas del reloj significa que se gira en la dirección opuesta a la dirección en la cual giran las manecillas de un reloj. Así, un punto que está encima del centro de rotación gira hacia la izquierda.
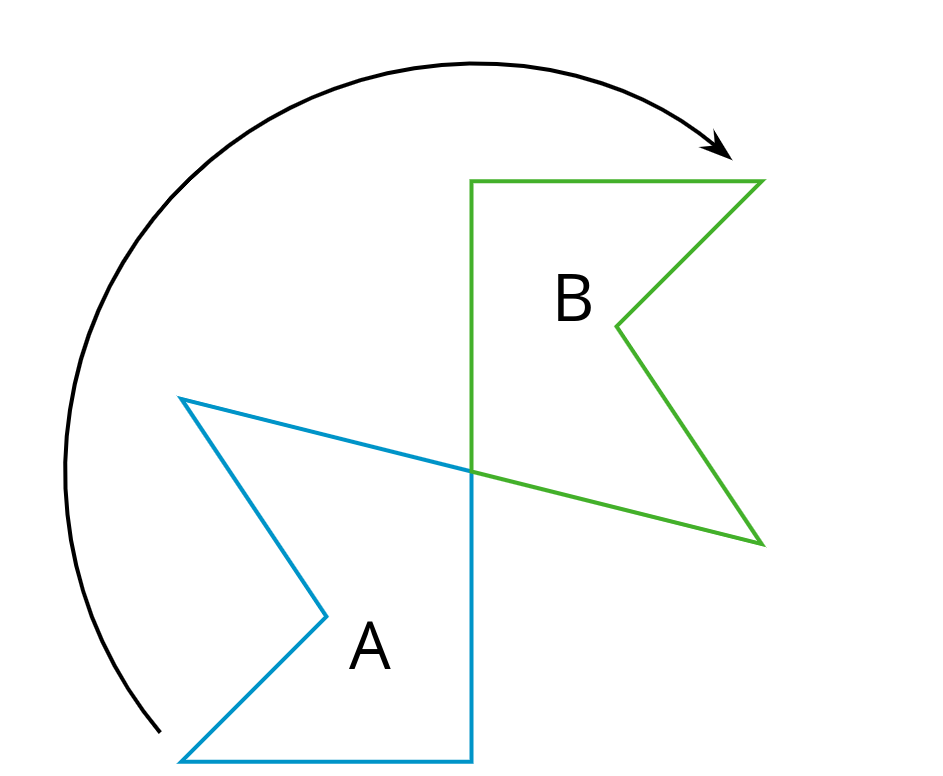
Este diagrama muestra como la figura A gira en el sentido contrario a las manecillas del reloj para formar a la figura B.
- en el sentido de las manecillas del reloj
En el sentido de las manecillas del reloj significa que se gira en la misma dirección que giran las manecillas de un reloj. Así, un punto que está encima del centro de rotación gira hacia la derecha. Este diagrama muestra como la figura A se giró en el sentido de las manecillas del reloj para formar la figura B.
- imagen
Una imagen es el resultado de aplicar traslaciones, rotaciones y reflexiones a un objeto. Cada parte del objeto original se mueve de la misma manera para coincidir con la parte correspondiente de la imagen.
En este diagrama, el triángulo \(ABC\) fue trasladado hacia arriba y hacia la derecha para forma el triángulo \(DEF\). El triángulo \(DEF\) es la imagen del triángulo original \(ABC\).
- reflexión
Una reflexión con respecto a una recta toma cada punto de una figura y lo mueve de manera perpendicular a un punto que está ubicado al lado opuesto de esa recta. El nuevo punto está a la misma distancia de la recta que el punto original.
Este diagrama muestra una reflexión de A con respecto a la recta \(\ell\) que produce la figura imagen B.
- rotación
Una rotación hace girar cada punto de una figura alrededor de un centro con un ángulo dado en una dirección específica.
Este diagrama muestra como al rotar el triángulo A alrededor del centro \(O\) con un ángulo de 55 grados en la dirección de las manecillas del reloj, se obtiene el triángulo B.
- traslación
Una traslación mueve cada punto de una figura cierta distancia en cierta dirección.
Este diagrama muestra cómo la figura A se traslada para obtener la figura B usando la dirección y la distancia indicadas por la flecha.
- vértice
Un vértice es un punto en donde dos o más aristas se encuentran. Los vértices de este polígono están etiquetados con las letras \(A\), \(B\), \(C\), \(D\) y \(E\).