Lección 6
Describamos transformaciones
Transformemos algunos polígonos en el plano de coordenadas.
6.1: Hallemos un centro de rotación
Andre realiza una rotación de 90 grados en el sentido contrario a las manecillas del reloj al polígono P y obtiene el polígono P', pero no dice cuál es el centro de rotación. ¿Puedes determinar el centro?
6.2: Falta de información: información sobre una transformación
Tu profesor te dará una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu compañero.
Si tu profesor te da la tarjeta de problema:
-
Lee tu tarjeta en silencio y piensa en lo que necesitas saber para poder contestar a la pregunta.
-
Pide a tu compañero la información específica que necesites.
-
Explica cómo estás usando la información para resolver el problema.
Sigue haciendo preguntas hasta que tengas suficiente información para solucionar el problema.
-
Comparte la tarjeta de problema y soluciona el problema independientemente.
-
Lee la tarjeta de datos y discute tu razonamiento.
Si tu profesor te da la tarjeta de datos:
-
Lee tu tarjeta en silencio.
-
Pregunta a tu compañero: “¿Qué información específica necesitas?” y espera a que te pida la información.
Si tu compañero te pide información que no está en la tarjeta, no hagas los cálculos por él. Dile que no tienes esa información.
-
Antes de compartir la información, pregunta “¿Por qué necesitas esa información?”. Escucha el razonamiento de tu compañero y haz preguntas que te ayuden a aclarar tus dudas.
-
Lee la tarjeta de problema y soluciona el problema independientemente.
-
Comparte la tarjeta de datos y discute tu razonamiento.
Haz una pausa acá para que tu profesor pueda revisar tu trabajo. Pide a tu profesor un nuevo juego de tarjetas y repite la actividad, intercambiando roles con tu compañero.
Algunas veces dos transformaciones, realizadas una después de la otra, se pueden describir como una sola transformación. Por ejemplo, en vez de trasladar 2 unidades hacia arriba y luego trasladar 3 unidades hacia arriba, podríamos simplemente trasladar 5 unidades hacia arriba. En vez de rotar 20 grados en sentido contrario a las manecillas del reloj alrededor del origen y luego rotar 80 grados en el sentido de las manecillas del reloj alrededor del origen, podríamos simplemente rotar 60 grados en el sentido de las manecillas del reloj alrededor del origen.
¿Puedes encontrar una descripción simple para reflejar con respecto al eje \(x\) y luego reflejar con respecto al eje \(y\)?
Resumen
El centro de rotación de una figura no tiene que ser necesariamente un punto de la figura. Para hallar un centro de rotación, busca un punto que esté a la misma distancia de dos puntos correspondientes. Para determinarlo con precisión, probablemente necesites hacer eso para distintos pares de puntos correspondientes.
Cuando realizamos una secuencia de transformaciones, el orden en que las realizamos es importante. Este es el triángulo \(ABC\) trasladado dos unidades hacia arriba y luego reflejado con respecto al eje \(x\).
Este es el triángulo \(ABC\) reflejado con respecto al eje \(x\) y luego trasladado dos unidades hacia arriba.
¡El triángulo \(ABC\) termina ubicado en posiciones diferentes cuando las transformaciones se realizan en el orden opuesto!
Entradas del glosario
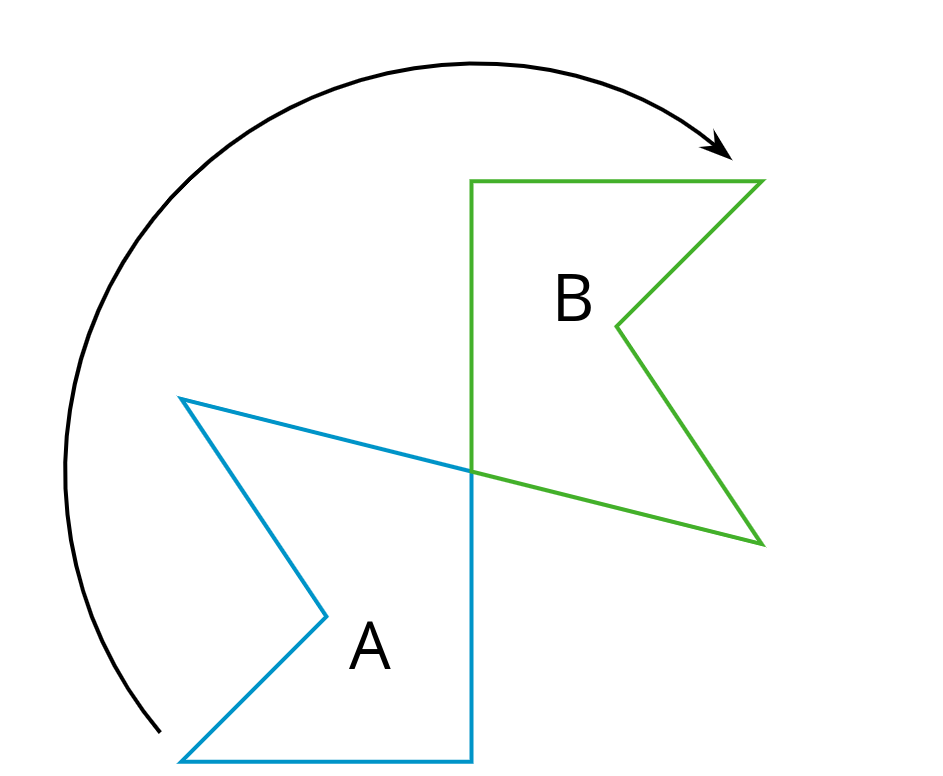
- en el sentido contrario a las manecillas del reloj
En el sentido contrario a las manecillas del reloj significa que se gira en la dirección opuesta a la dirección en la cual giran las manecillas de un reloj. Así, un punto que está encima del centro de rotación gira hacia la izquierda.
Este diagrama muestra como la figura A gira en el sentido contrario a las manecillas del reloj para formar a la figura B.
- en el sentido de las manecillas del reloj
En el sentido de las manecillas del reloj significa que se gira en la misma dirección que giran las manecillas de un reloj. Así, un punto que está encima del centro de rotación gira hacia la derecha. Este diagrama muestra como la figura A se giró en el sentido de las manecillas del reloj para formar la figura B.
- imagen
Una imagen es el resultado de aplicar traslaciones, rotaciones y reflexiones a un objeto. Cada parte del objeto original se mueve de la misma manera para coincidir con la parte correspondiente de la imagen.
En este diagrama, el triángulo \(ABC\) fue trasladado hacia arriba y hacia la derecha para forma el triángulo \(DEF\). El triángulo \(DEF\) es la imagen del triángulo original \(ABC\).
- plano de coordenadas
El plano de coordenadas es un sistema para especificar la ubicación de puntos. Por ejemplo, el punto \(R\) está ubicado en \((3, 2)\) en el plano de coordenadas, porque está tres unidades a la derecha y dos unidades arriba del origen.
- reflexión
Una reflexión con respecto a una recta toma cada punto de una figura y lo mueve de manera perpendicular a un punto que está ubicado al lado opuesto de esa recta. El nuevo punto está a la misma distancia de la recta que el punto original.
Este diagrama muestra una reflexión de A con respecto a la recta \(\ell\) que produce la figura imagen B.
- rotación
Una rotación hace girar cada punto de una figura alrededor de un centro con un ángulo dado en una dirección específica.
Este diagrama muestra como al rotar el triángulo A alrededor del centro \(O\) con un ángulo de 55 grados en la dirección de las manecillas del reloj, se obtiene el triángulo B.
- secuencia de transformaciones
Una secuencia de transformaciones es un conjunto de traslaciones, rotaciones, reflexiones y dilataciones de una figura, que se realizan en un orden dado.
Este diagrama muestra una secuencia de transformaciones que lleva la figura A a la figura C.
Primero, A se traslada hacia la derecha para formar B. Luego, B se refleja con respecto a la recta \(\ell\) para formar C.
- transformación
Una transformación es una traslación, una rotación, una reflexión, una dilatación o una combinación de ellas.
- traslación
Una traslación mueve cada punto de una figura cierta distancia en cierta dirección.
Este diagrama muestra cómo la figura A se traslada para obtener la figura B usando la dirección y la distancia indicadas por la flecha.
- vértice
Un vértice es un punto en donde dos o más aristas se encuentran. Los vértices de este polígono están etiquetados con las letras \(A\), \(B\), \(C\), \(D\) y \(E\).