Lección 2
Puntos en la recta numérica
Grafiquemos números positivos y negativos en la recta numérica.
2.1: Un punto en la recta numérica
¿Cuáles de los siguientes números podría ser \(B\)?
2.5
\(\frac25\)
\(\frac{5}{2}\)
\(\frac{25}{10}\)
2.49
2.2: ¿Cuál es la temperatura?
-
Estos son cinco termómetros. Los primeros cuatro termómetros muestran las temperaturas en grados Celsius. Escribe las temperaturas en los espacios en blanco.
Al último termómetro le hacen falta algunos números. Escríbelos en las cajas.
-
Elena dice que el termómetro que se muestra aquí indica \(\text-2.5^\circ \text{C}\) porque la línea del líquido está por encima de \(\text-2^\circ \text{C}\). Jada dice que indica \(\text-1.5^\circ \text{C}\). ¿Estás de acuerdo con alguna de ellas? Explica tu razonamiento.
- Una mañana en Phoenix, Arizona, la temperatura era \(8^\circ \text{C}\) y la temperatura en Portland, Maine, era \(12^\circ \text{C}\) más fría. ¿Cuál era la temperatura en Portland?
2.3: Rectas numéricas doblables
Tu profesor te dará una hoja de papel de calcar para dibujar sobre ella una recta numérica.
-
Sigue los siguientes pasos para hacer tu propia recta numérica.
- Usa una regla para dibujar una recta horizontal. Señala la mitad de la recta y etiquétala 0.
- Dibuja marcas a la derecha del 0 que estén separadas por 1 centímetro. Etiqueta las marcas 1, 2, 3. . . 10. Esto representa el lado positivo de tu recta numérica.
- Dobla tu papel de tal forma que un doblez vertical pase por el 0 y que los dos lados de la recta numérica coincidan perfectamente.
- Usa el doblez para ayudarte a calcar las marcas que ya dibujaste en el lado opuesto de la recta numérica. Desdobla y etiqueta las marcas -1, -2, -3. . . -10. Esto representa el lado negativo de tu recta numérica.
-
Usa tu recta numérica para contestar estas preguntas:
- ¿Cuál número está a la misma distancia de cero que el número 4?
- ¿Cuál número está a la misma distancia de cero que el número -7?
- Dos números que están a la misma distancia del cero en la recta numérica se llaman opuestos. Encuentra otro par de opuestos en la recta numérica.
- Determina qué tan lejos está el número 5 de 0. Después elige un numero positivo y un número negativo que estén más lejos del 0 que el número 5.
- Determina qué tan lejos está el número -2 de 0. Después elige un numero positivo y un número negativo que estén más lejos del 0 que el número -2.
Haz una pausa para que tu profesor pueda revisar tu trabajo.
-
Esta es una recta numérica con algunos puntos etiquetados con letras. Determina la ubicación de los puntos \(P\), \(X\) y \(Y\).
Si te bloqueas, calca la recta numérica y los puntos sobre una hoja de papel de calcar, dóblalo de tal forma que el doblez vertical pase por 0 y usa la recta numérica doblada para ayudarte a encontrar los valores desconocidos.
Al mediodía, las temperaturas en Portland, Maine, y Phoenix, Arizona, tenían valores opuestos. La temperatura en Portland era \(18^\circ \text{C}\) menos que en Phoenix. ¿Cuál era la temperatura en cada ciudad? Explica tu razonamiento.
Resumen
Esta es una recta numérica etiquetada con números positivos y negativos. El número 4 es positivo, así que su ubicación es 4 unidades a la derecha del 0 en la recta numérica. El número -1.1 es negativo así que su ubicación es 1.1 unidades a la izquierda del 0 en la recta numérica.
Decimos que el opuesto de 8.3 es -8.3 y el opuesto de \(\frac {\text{-}3}{2}\) es \(\frac32\). Cualquier par de números que estén ubicados a la misma distancia del 0 se llaman opuestos.
Los puntos \(A\) y \(B\) son opuestos porque ambos están a 2.5 unidades del 0, aunque \(A\) está a la izquierda del 0 y \(B\) está a la derecha del 0.
Un número positivo tiene por opuesto un número negativo. Un número negativo tiene por opuesto un número positivo. El opuesto de 0 es 0.
Has trabajado con números positivos durante muchos años. Todos los números positivos que has visto, número enteros y no enteros, se pueden pensar como fracciones y se pueden ubicar en una recta numérica.
Para ubicar un número no entero en una recta numérica podemos dividir la distancia entre dos números enteros en partes fraccionarias y después contar el número de partes. Por ejemplo, 2.7 se puede escribir como \(2 \frac {7}{10}\). El segmento entre 2 y 3 se puede dividir en 10 partes iguales o 10 décimas. Desde 2, podemos contar 7 de las décimas para ubicar 2.7 en la recta numérica.
Todas las fracciones y sus opuestos son lo que llamamos números racionales. Por ejemplo, 4, -1.1, 8.3, -8.3, \(\frac {\text{-}3}{2}\) y \(\frac32\) son todos números racionales.
Entradas del glosario
- número negativo
Un número negativo es un número que es menor que cero. En la recta numérica horizontal, los números negativos usualmente se muestran a la izquierda del 0.
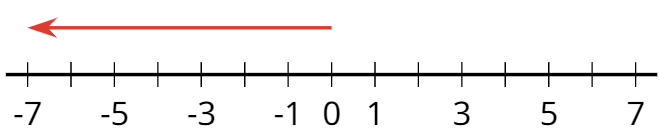
- número positivo
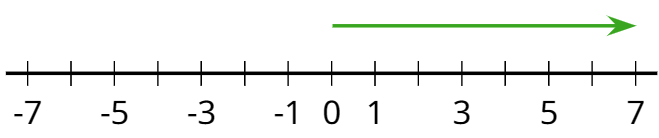
Un número positivo es un número que es mayor que cero. En la recta numérica horizontal, los números positivos usualmente se muestran a la derecha del 0.
- número racional
Un número racional es una fracción o el opuesto de una fracción.
Por ejemplo, 8 y -8 son números racionales porque se pueden escribir como \(\frac81\) y \(\text-\frac81\).
Los números 0.75 y -0.75 también son números racionales porque se pueden escribir como \(\frac{75}{100}\) y \(\text-\frac{75}{100}\).
- opuestos
Dos números son opuestos si al ubicarlos sobre la recta numérica están a lados opuestos del 0 pero a la misma distancia del 0.
Por ejemplo, 4 es el opuesto de -4 y -4 es el opuesto de 4. Ambos están a la misma distancia de 0. Uno de ellos es negativo y el otro es positivo.