Lección 5
Usemos números negativos para dar sentido a contextos
Demos sentido a las cantidades negativas de dinero.
5.1: Observa y pregúntate: va y viene
| actividad | cantidad |
|---|---|
| hacer mis tareas del hogar | 30.00 |
| cuidar a mi primo | 45.00 |
| comprar mi almuerzo | -10.80 |
| recibir mi mesada | 15.00 |
| comprar un camisa | -18.69 |
| acariciar a mi perro | 0.00 |
¿Qué observas? ¿Qué te preguntas?
5.2: El puesto de comida
La gerente de un puesto de comida lleva un registro de todos los insumos que compra y todos los productos que vende. La tabla muestra algunos de sus registros del martes.
| artículo | cantidad | valor en dólares |
|---|---|---|
| Rosquillas | -58 | 37.70 |
| Popotes | 3,000 | -10.35 |
| Perros calientes | -39 | 48.75 |
| Pizza | 13 | -116.87 |
| Manzanas | -40 | 14.00 |
| Papas a la francesa | -88 | 132.00 |
- ¿Qué artículos vendió ella? Explica tu razonamiento.
- ¿Cómo podemos interpretar -58 en esta situación?
- ¿Cómo podemos interpretar -10.35 en esta situación?
- ¿En qué artículo gastó ella la mayor cantidad de dinero? Explica tu razonamiento.
5.3: Bebidas a la venta
Una máquina dispensadora en un edificio de oficinas vende bebidas embotelladas. La máquina lleva el registro de todos los cambios en el número de botellas que se dan debido a ventas, recargas y mantenimiento. Este registro muestra los cambios por cada período de 5 minutos durante una hora.
-
¿Qué puede indicar un número positivo en ese contexto?, ¿y un número negativo?
-
¿Qué indicaría en este contexto un "0" en la segunda columna?
-
¿Qué números, positivos o negativos, dan como resultado una menor cantidad de botellas en la máquina?
- ¿A qué hora se presentó el cambio más grande en el número de botellas en la máquina? ¿Cómo influyó este cambio en el número de botellas restantes en la máquina?
- ¿En qué período, de 8:05 a 8:09 o de 8:25 a 8:29, hubo un cambio más grande en el número de botellas en la máquina? Explica tu razonamiento.
- La máquina debe vaciarse para hacerle mantenimiento. Si hay 40 botellas en la máquina en el momento del mantenimiento, ¿qué número irá en la segunda columna de la tabla?
| hora | número de botellas |
|---|---|
| 8:00–8:04 | -1 |
| 8:05–8:09 | +12 |
| 8:10–8:14 | -4 |
| 8:15–8:19 | -1 |
| 8:20–8:24 | -5 |
| 8:25–8:29 | -12 |
| 8:30–8:34 | -2 |
| 8:35–8:39 | 0 |
| 8:40–8:44 | 0 |
| 8:45–8:49 | -6 |
| 8:50–8:54 | +24 |
| 8:55–8:59 | 0 |
| mantenimiento |
Priya, Mai y Lin fueron a un café un fin de semana. Su cuenta conjunta fue de \$25. Cada estudiante le dio al mesero un billete de \$10. El mesero tomó estos \$30 y trajo de cambio cinco billetes de \$1. Cada estudiante tomó \$1, dejando el resto, \$2, como propina para el mesero.
Al alejarse del café, Lin pensó: "Un momento, esto no tiene sentido. Yo puse \$10 y me devolvieron \$1, así que terminé pagando \$9. Lo mismo le pasó a Mai y Priya. Entre todas, pagamos \$27. Dejamos \$2 de propina. Eso da un total de \$29. Pero originalmente le dimos \$30 al mesero. ¿Qué pasó con el dólar que hace falta?".
Piensa sobre la situación y la pregunta de Lin. ¿Estás de acuerdo en que los números no coinciden con la cantidad adecuada? Explica tu razonamiento.
Resumen
A veces representamos cambios en una cantidad usando números positivos y negativos. Si la cantidad aumenta, el cambio es positivo. Si la cantidad disminuye, el cambio es negativo.
- Supongamos que se ponen 5 galones de agua en una lavadora. Podemos representar el cambio en el número de galones como +5. Si se sacan 3 galones de la lavadora, representamos el cambio como -3.
Es especialmente común representar dinero que recibimos con números positivos y dinero que gastamos con números negativos.
- Supongamos que Clare recibe $30.00 por su cumpleaños y gasta $18.00 comprando almuerzo para ella y una amiga. Para ella, el valor del regalo se puede representar como +30.00 y el valor del almuerzo como -18.00.
Que un número sea considerado positivo o negativo depende de la perspectiva de la persona. Si la abuela de Clare le da $20 por su cumpleaños, Clare puede ver esto como +20 porque para ella la cantidad de dinero que tiene ha aumentado. Pero su abuela puede ver esto como -20, porque para ella, la cantidad de dinero que tenía ha disminuido.
En general, al usar números positivos y negativos para representar cambios, tenemos que ser muy claros sobre qué quiere decir un cambio positivo y qué quiere decir un cambio negativo.
Entradas del glosario
- número negativo
Un número negativo es un número que es menor que cero. En la recta numérica horizontal, los números negativos usualmente se muestran a la izquierda del 0.
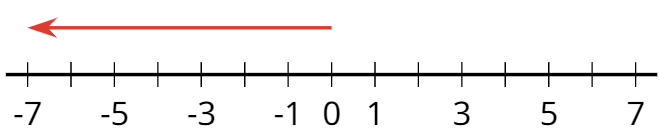
- número positivo
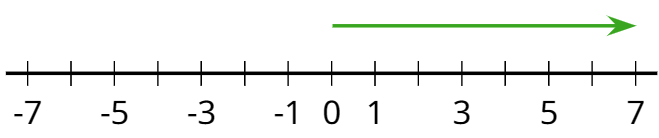
Un número positivo es un número que es mayor que cero. En la recta numérica horizontal, los números positivos usualmente se muestran a la derecha del 0.
- número racional
Un número racional es una fracción o el opuesto de una fracción.
Por ejemplo, 8 y -8 son números racionales porque se pueden escribir como \(\frac81\) y \(\text-\frac81\).
Los números 0.75 y -0.75 también son números racionales porque se pueden escribir como \(\frac{75}{100}\) y \(\text-\frac{75}{100}\).
- opuestos
Dos números son opuestos si al ubicarlos sobre la recta numérica están a lados opuestos del 0 pero a la misma distancia del 0.
Por ejemplo, 4 es el opuesto de -4 y -4 es el opuesto de 4. Ambos están a la misma distancia de 0. Uno de ellos es negativo y el otro es positivo.
- signo
El signo de cualquier número distinto de cero es positivo o negativo.
Por ejemplo, el signo de 6 es positivo. El signo de -6 es negativo. El cero no tiene signo, porque no es positivo ni negativo.