Lección 6
Valor absoluto de números
Exploremos distancias al cero más de cerca.
6.1: Conversación numérica: más cerca de cero
Para cada pareja de expresiones, decide mentalmente cuál tiene un valor que esté más cerca al 0.
\(\frac{9}{11}\) o \(\frac{15}{11}\)
\(\frac15\) o \(\frac19\)
\(1.25\) o \(\frac54\)
\(0.01\) o \(0.001\)
6.2: Pulga saltarina
-
- Si la pulga empieza en 1 y salta 4 unidades hacia la derecha, ¿dónde termina? ¿qué tan lejos del 0 es esto?
- Si la pulga empieza en 1 y salta 4 unidades hacia la izquierda, ¿dónde termina? ¿qué tan lejos del 0 es esto?
- Si la pulga empieza en 0 y salta alejándose 3 unidades, ¿dónde puede aterrizar?
- Si la pulga salta 7 unidades y aterriza en 0, ¿dónde pudo haber empezado?
- El valor absoluto de un número es la distancia a la que está de 0. En este momento, la pulga está a la derecha del 0 y el valor absoluto de su ubicación es 4. ¿Dónde está en la recta numérica?
- Si la pulga está a la izquierda del 0 y el valor absoluto de su ubicación es 5, ¿dónde está en la recta numérica?
- Si la pulga está a la derecha del 0 y el valor absoluto de su ubicación es 2.5, ¿dónde está en la recta numérica?
- Si la pulga empieza en 1 y salta 4 unidades hacia la derecha, ¿dónde termina? ¿qué tan lejos del 0 es esto?
-
Usamos la notación \(|{\text-2}|\) para decir "el valor absoluto de -2", lo cual significa "la distancia de -2 al 0 en la recta numérica".
- ¿Qué quiere decir \(|\text-7|\) y cuál es su valor?
- ¿Qué quiere decir \(|{1.8}|\) y cuál es su valor?
6.3: Altitud y temperatura absoluta
-
Una parte de la ciudad de Nueva Orleans está 6 pies por debajo del nivel del mar. Podemos usar "-6 pies" para describir su altitud y "\(|\text-6|\) pies" para describir su distancia vertical al nivel del mar. En el contexto de la altitud, ¿qué describiría cada uno de los siguientes números?
- 25 pies
- \(|25|\) pies
- -8 pies
- \(|\text-8|\) pies
- La altitud de una ciudad tiene una diferencia de 10 pies con el nivel del mar. Escribe las dos altitudes que podría tener la ciudad.
-
Escribimos "\(\text-5^\circ \text{C}\)" para describir una temperatura que está 5 grados Celsius por debajo del punto de congelación y "\(5^\circ \text{C}\)" para una temperatura que está 5 grados por encima del punto de congelación. En este contexto, ¿qué describiría cada uno de los siguientes números?
- \(1^\circ \text{C}\)
- \(\text-4^\circ \text{C}\)
- \(|12|^\circ \text{C}\)
- \(|\text-7|^\circ \text{C}\)
-
-
¿Cuál temperatura es más fría: \(\text-6^\circ \text{C}\) o \(3^\circ \text{C}\)?
-
¿Cuál temperatura es más cercana a la temperatura del punto de congelación: \(\text-6^\circ \text{C}\) o \(3^\circ \text{C}\)?
-
¿Cuál temperatura tiene un valor absoluto más pequeño? Explica cómo lo sabes.
-
En cierto momento, la diferencia entre la temperatura en la ciudad de Nueva York y en Boston era 7 grados Celsius. La diferencia entre la temperatura en Boston y en Chicago también era 7 grados Celsius. ¿La temperatura en Nueva York era la misma temperatura que en Chicago? Explica tu respuesta.
Resumen
Para comparar números, comparamos sus posiciones en la recta numérica: el que esté más hacia la derecha es mayor; el que esté más hacia la izquierda es menor.
Algunas veces queremos comparar cuál está más cerca o más lejos del cero. Por ejemplo, puede que queramos saber qué tan lejos está la temperatura del punto de congelación \(0 ^\circ \text{C}\), sin importar si está por encima o por debajo de este punto.
El valor absoluto de un número nos indica su distancia al 0.
El valor absoluto de -4 es 4 porque -4 está 4 unidades a la izquierda del 0. El valor absoluto de 4 también es 4, porque 4 está 4 unidades a la derecha del 0. Los opuestos siempre tienen el mismo valor absoluto porque ambos están a la misma distancia del 0.
La distancia de 0 hasta sí mismo es 0, así que el valor absoluto de 0 es 0. Cero es el único número cuya distancia al 0 es 0. Para los demás valores absolutos, siempre hay dos números, uno positivo y uno negativo, que están a la misma distancia del 0.
Para decir "el valor absoluto de 4", escribimos: \(\displaystyle |4|\)
Para decir que "el valor absoluto de -8 es 8", escribimos: \(\displaystyle |\text- 8| = 8\)
Entradas del glosario
- número negativo
Un número negativo es un número que es menor que cero. En la recta numérica horizontal, los números negativos usualmente se muestran a la izquierda del 0.
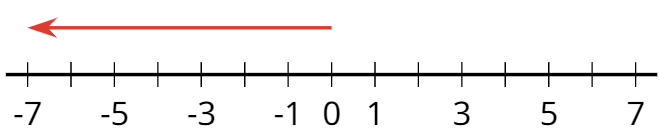
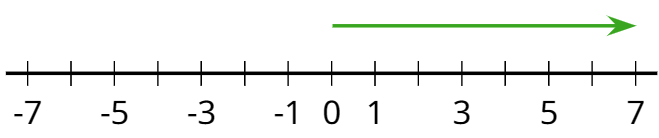
- número positivo
Un número positivo es un número que es mayor que cero. En la recta numérica horizontal, los números positivos usualmente se muestran a la derecha del 0.
- número racional
Un número racional es una fracción o el opuesto de una fracción.
Por ejemplo, 8 y -8 son números racionales porque se pueden escribir como \(\frac81\) y \(\text-\frac81\).
Los números 0.75 y -0.75 también son números racionales porque se pueden escribir como \(\frac{75}{100}\) y \(\text-\frac{75}{100}\).
- opuestos
Dos números son opuestos si al ubicarlos sobre la recta numérica están a lados opuestos del 0 pero a la misma distancia del 0.
Por ejemplo, 4 es el opuesto de -4 y -4 es el opuesto de 4. Ambos están a la misma distancia de 0. Uno de ellos es negativo y el otro es positivo.
- signo
El signo de cualquier número distinto de cero es positivo o negativo.
Por ejemplo, el signo de 6 es positivo. El signo de -6 es negativo. El cero no tiene signo, porque no es positivo ni negativo.
- valor absoluto
El valor absoluto de un número es su distancia al 0 en la recta numérica.
El valor absoluto de -7 es 7, porque -7 está a 7 unidades del 0. El valor absoluto de 5 es 5, porque 5 está a 5 unidades del 0.