Lección 7

Comparemos números y distancias al cero

Usemos el valor absoluto y los números negativos para pensar sobre altitud.

7.1: Opuestos

  1. \(a\) es un número racional. Escoge un valor para \(a\) y ubícalo en la recta numérica.

    Blank number line, 21 evenly spaced tick marks, middle tick mark labeled zero.
    1. Según donde ubicaste \(a\), ubica \(\text- a\) en la misma recta numérica.
    2. ¿Cuál es el valor de \(\text- a\) que ubicaste?
  3. Noah dijo: "Si \(a\) es un número racional, \(\text- a\) siempre será un número negativo". ¿Estás de acuerdo con Noah? Explica tu razonamiento.

7.2: Submarino

Un submarino está a una altitud de -100 pies (100 pies por debajo del nivel del mar). Comparemos las altitudes de estas cuatro personas con la del submarino:

  • La altitud de Clare es mayor que la altitud del submarino. Clare está más lejos del nivel del mar que el submarino.
  • La altitud de Andre es menor que la altitud del submarino. Andre está más lejos del nivel del mar que el submarino.
  • La altitud de Han es mayor que la altitud del submarino. Han está más cerca del nivel del mar que el submarino.
  • La altitud de Lin está a la misma distancia del nivel del mar que el submarino.
  1. Completa la tabla de la siguiente forma.
    1. Escribe una altitud posible para cada persona.
    2. Usa \(<\), \(>\) o \(=\) para comparar la altitud de esa persona con la del submarino.
    3. Usa el valor absoluto para expresar qué tan lejos está la persona del nivel del mar (altitud 0).
    Como ejemplo, la primera fila se ha completado con una altitud posible para Clare.
      altitud posible comparada con el submarino distancia a partir del nivel del mar
    Clare 150 pies \(150 > \text-100\) \(|150|\) o 150 pies
    Andre      
    Han      
    Lin      
  2. Priya dice que su altitud es menor que la del submarino y que ella está más cerca del nivel del mar. ¿Esto es posible? Explica tu razonamiento.

7.3: Falta de información: puntos en la recta numérica

Tu profesor te dará una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu compañero.

Si tu profesor te da la tarjeta de problema:

  1. Lee tu tarjeta en silencio y piensa en lo que necesitas saber para poder contestar a la pregunta.

  2. Pide a tu compañero la información específica que necesites.

  3. Explica cómo estás usando la información para resolver el problema.

    Sigue haciendo preguntas hasta que tengas suficiente información para solucionar el problema.

  4. Comparte la tarjeta de problema y soluciona el problema independientemente.

  5. Lee la tarjeta de datos y discute tu razonamiento.

Si tu profesor te da la tarjeta de datos:

  1. Lee tu tarjeta en silencio.

  2. Pregunta a tu compañero: “¿Qué información específica necesitas?” y espera a que te pida la información.

    Si tu compañero te pide información que no está en la tarjeta, no hagas los cálculos por él. Dile que no tienes esa información.

  3. Antes de compartir la información, pregunta “¿Por qué necesitas esa información?”. Escucha el razonamiento de tu compañero y haz preguntas que te ayuden a aclarar tus dudas.

  4. Lee la tarjeta de problema y soluciona el problema independientemente.

  5. Comparte la tarjeta de datos y discute tu razonamiento.

Haz una pausa acá para que tu profesor pueda revisar tu trabajo. Pide a tu profesor un nuevo juego de tarjetas y repite la actividad, intercambiando roles con tu compañero.

7.4: Mezclar y combinar desigualdades

Estos son algunos números y símbolos de desigualdad. Trabaja con tu compañero para escribir afirmaciones verdaderas de comparación.

-0.7

\(\text{-}\frac {3}{5}\)

1

4

\(|\text-8|\)

\(<\)

\(\text{-}\frac {6}{3}\)

-2.5

2.5

8

\(|0.7|\)

\(=\)

-4

0

\(\frac72\)

\(|3|\)

\(|\text{-}\frac {5}{2}|\)

\(>\)

Uno de ustedes debe escoger dos números y un símbolo de comparación y usarlos para escribir una afirmación verdadera usando los símbolos. El otro debe escribir una oración en palabras con el mismo significado, usando las siguientes frases:

  • es igual a
  • es el valor absoluto de
  • es mayor que
  • es menor que

Por ejemplo, uno puede escribir \(4 < 8\) y el otro escribirá, "4 es menor que 8". Intercambien roles hasta que cada uno tenga tres afirmaciones matemáticas verdaderas y tres oraciones escritas.



Para cada pregunta, escoge un valor para cada variable de tal forma que todo el enunciado sea verdadero (cuando se usa la palabra y en matemáticas, ambas partes deben ser verdaderas para que todo el enunciado sea verdadero). ¿Puedes hacerlo si una variable es negativa y una es positiva? ¿Puedes hacerlo si ambos valores son negativos?

  1. \(x < y\) y \(|x| < y\).
  2. \(a < b\) y \(|a| < |b|\).
  3. \(c < d\) y \(|c| > d\).
  4. \(t < u\) y \(|t| > |u|\).

Resumen

Usar la altitud nos puede ayudar a comparar dos números racionales o dos valores absolutos.

  • Supongamos que un ancla está a una altitud de -10 metros y una casa está a una altitud de 12 metros. Para describir que el ancla está a una altitud menor que la casa, podemos escribir \(\text-10<12\) y decimos "-10 es menor que 12".
  • El ancla está más cerca que la casa del nivel del mar (o altitud 0). Para describir esto, escribimos \(|\text-10|<|12|\) y decimos "la distancia entre -10 y 0 es menor que la distancia entre 12 y 0". 

Podemos usar descripciones similares para comparar números racionales y sus valores absolutos fuera del contexto de altitud.

  • Para comparar la distancia de -47.5 y 5.2 al 0, podemos decir: \(|\text-47.5|\) está a 47.5 unidades del 0 y \(|5.2|\) está a 5.2 unidades del 0, así \(|\text-47.5|>|5.2|\).
  • \(|\text-18|>4\) significa que el valor absoluto de -18 es mayor que 4. Esto es verdad porque 18 es mayor que 4.

Entradas del glosario

  • número negativo

    Un número negativo es un número que es menor que cero. En la recta numérica horizontal, los números negativos usualmente se muestran a la izquierda del 0.

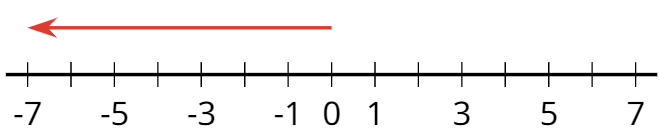
  • número positivo

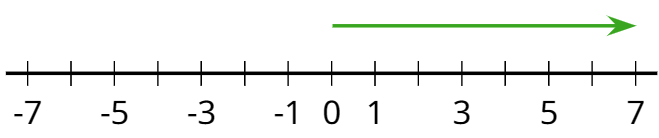
    Un número positivo es un número que es mayor que cero. En la recta numérica horizontal, los números positivos usualmente se muestran a la derecha del 0.

  • número racional

    Un número racional es una fracción o el opuesto de una fracción.

    Por ejemplo, 8 y -8 son números racionales porque se pueden escribir como  \(\frac81\) y \(\text-\frac81\).

    Los números 0.75 y -0.75 también son números racionales porque se pueden escribir como  \(\frac{75}{100}\) y \(\text-\frac{75}{100}\).

  • opuestos

    Dos números son opuestos si al ubicarlos sobre la recta numérica están a lados opuestos del 0 pero a la misma distancia del 0.

    Por ejemplo, 4 es el opuesto de -4 y -4 es el opuesto de 4. Ambos están a la misma distancia de 0. Uno de ellos es negativo y el otro es positivo.

    Number line that extends from -5 to 5, with points at -4 and 4.
  • signo

    El signo de cualquier número distinto de cero es positivo o negativo.

    Por ejemplo, el signo de 6 es positivo. El signo de -6 es negativo. El cero no tiene signo, porque no es positivo ni negativo.

  • valor absoluto

    El valor absoluto de un número es su distancia al 0 en la recta numérica.

    Horizontal number line, tick marks every 1 unit from -7 to 7. Above, there is a horizontal segment from -7 to 0 labeled 7, and a horizontal segment from 0 to 5 labeled 5. 

    El valor absoluto de -7 es 7, porque -7 está a 7 unidades del 0. El valor absoluto de 5 es 5, porque 5 está a 5 unidades del 0.