Lección 4
Ordenemos números racionales
Ordenemos números racionales.
4.1: Comparemos números
Usa los símbolos >, <, o = para comparar cada pareja de números. Prepárate para explicar tu razonamiento.
- 12 _____ 19
- 212 _____ 190
- 15 _____ 1.5
- 9.02 _____ 9.2
- 6.050 _____ 6.05
- 0.4 _____ \(\frac{9}{40}\)
- \(\frac{19}{24}\) _____ \(\frac{19}{21}\)
- \(\frac{16}{17}\) _____ \(\frac{11}{12}\)
4.2: Ordenemos tarjetas con números racionales
Tu profesor te dará una colección de tarjetas con números. Ordénalas de menor a mayor.
Tu profesor te dará una segunda colección de tarjetas con números. Añádelas en los lugares correctos en la colección ordenada.
4.3: Comparación de puntos en una recta
-
Usa cada uno de los siguientes términos por lo menos una vez para describir o comparar los valores de los puntos \(M\), \(N\), \(P\), \(R\).
- mayor que
- menor que
- opuesto de (u opuestos)
- número negativo
-
Cuál sería el valor de los otros puntos si:
- \(P\) es \(2\frac12\)
- \(N\) es -0.4
- \(R\) es 200
- \(M\) es -15
La lista de fracciones entre 0 y 1 con denominador entre 1 y 3 se ve de esta manera: \(\displaystyle \frac{0}{1}, \, \frac{1}{1},\, \frac{1}{2},\, \frac{1}{3},\, \frac{2}{3}\) Podemos ordenarlas de esta manera: :\(\displaystyle \frac{0}{1} < \frac{1}{3} < \frac{1}{2} < \frac{2}{3} < \frac{1}{1}\)
Ahora, expandamos la lista para incluir fracciones con denominador 4. No incluiremos \(\frac{2}{4}\) porque \(\frac{1}{2}\) ya está en la lista. \(\displaystyle \frac{0}{1} <\frac{1}{4} < \frac{1}{3} < \frac{1}{2} < \frac{2}{3} < \frac{3}{4} < \frac{1}{1}\)
- Expande la lista de nuevo para incluir fracciones que tengan denominador 5.
- Expande la lista que hiciste para incluir fracciones que tienen denominador 6.
- Cuando añades una nueva fracción a la lista, la pones en medio de dos "vecinos". Vuelve y observa detenidamente tu trabajo. ¿Ves alguna relación entre una nueva fracción y sus dos vecinos?
Resumen
Para ordenar números racionales del menor al mayor, los listamos en el orden en que aparecen en la recta numérica de izquierda a derecha. Por ejemplo, podemos ver que los números:
-2.7, -1.3, 0.8
están listados del menor al mayor debido al orden en que ellos aparecen en la recta numérica.
Entradas del glosario
- número negativo
Un número negativo es un número que es menor que cero. En la recta numérica horizontal, los números negativos usualmente se muestran a la izquierda del 0.
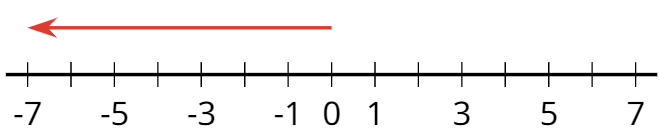
- número positivo
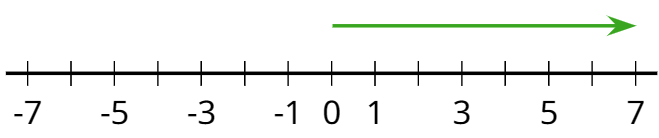
Un número positivo es un número que es mayor que cero. En la recta numérica horizontal, los números positivos usualmente se muestran a la derecha del 0.
- número racional
Un número racional es una fracción o el opuesto de una fracción.
Por ejemplo, 8 y -8 son números racionales porque se pueden escribir como \(\frac81\) y \(\text-\frac81\).
Los números 0.75 y -0.75 también son números racionales porque se pueden escribir como \(\frac{75}{100}\) y \(\text-\frac{75}{100}\).
- opuestos
Dos números son opuestos si al ubicarlos sobre la recta numérica están a lados opuestos del 0 pero a la misma distancia del 0.
Por ejemplo, 4 es el opuesto de -4 y -4 es el opuesto de 4. Ambos están a la misma distancia de 0. Uno de ellos es negativo y el otro es positivo.
- signo
El signo de cualquier número distinto de cero es positivo o negativo.
Por ejemplo, el signo de 6 es positivo. El signo de -6 es negativo. El cero no tiene signo, porque no es positivo ni negativo.