Lección 3

Comparemos números positivos y negativos

Comparemos números en la recta numérica.

3.1: Cuál es diferente: desigualdades

¿Cuál desigualdad es diferente?

  • \(\frac{5}{4} < 2\)
  • \(8.5 > 0.95\)
  • \(8.5 < 7\)
  • \(10.00 < 100\)

3.2: Comparemos temperaturas

Estas son las temperaturas bajas, en grados Celsius, de una semana en Anchorage, Alaska.

día lu ma mi ju vi sa do
temperatura 5 -1 -5.5 -2 3 4 0
  1. Grafica las temperaturas en una recta numérica. ¿Qué día de la semana tuvo la temperatura más baja?

  2. La temperatura más baja jamás registrada en los Estados Unidos fue -62 grados Celsius, en Prospect Creek Camp, Alaska. La temperatura promedio en Marte es alrededor de -55 grados Celsius.

    1. ¿Es más caliente la temperatura promedio en Marte o la temperatura más fría registrada en los Estados Unidos? Explica cómo lo sabes.
    2. Escribe una desigualdad para mostrar tu respuesta.

  3. En un día de invierno la temperatura más baja en Anchorage, Alaska fue -21 grados Celsius y la temperatura más baja en Mineápolis, Minnesota fue -14 grados Celsius.

    Jada dijo: "Sé que 14 es menor que 21, así que -14 también es menor que -21. Esto significa que hizo más frío en Mineápolis que en Anchorage".

    ¿Estás de acuerdo? Explica tu razonamiento.



Otra escala de temperatura que se usa frecuentemente en ciencia es la escala Kelvin. En esta escala, la temperatura más baja posible es 0 y corresponde a -273.15 grados en la escala Celsius. Cada incremento de \(1\text{ K}\) es lo mismo que un incremento de \(1 ^\circ\text{C}\), así que \(10\text{ K}\) es lo mismo que \(\text-263.15 ^\circ\text{C}\).

  1. El agua hierve a \(100^\circ \text{C}\). ¿Cuánto es esta temperatura en \(\text{K}\)?
  2. El amoníaco hierve a \(\text-35.5^\circ \text{C}\). ¿Cuál es el punto de ebullición del amoníaco en \(\text{K}\)?
  3. Explica por qué solo se necesitan números positivos (y 0) para registrar temperaturas en \(\text{K}\).

3.3: Números racionales en la recta numérica

  1. Ubica los números -2, 4, -7 y 10 en la recta numérica. Etiqueta cada punto con su valor numérico.

    Number line, 21 evenly spaced tick marks, middle tick mark labeled 0, next labeled 1, the rest blank.

  2. Decide si cada enunciado de desigualdad es verdadero o falso. Prepárate para explicar tu razonamiento.

    1. \(\text-2 < 4\)
    2. \(\text-2 < \text-7\)
    3. \(4 > \text-7\)
    4. \(\text-7 > 10\)
  3. Andre dice que \(\frac14\) es menor que \(\text{-}\frac {3}{4}\) porque, de los dos números, \(\frac14\) está más cerca del 0. ¿Estás de acuerdo? Explica tu razonamiento.

  4. Contesta cada pregunta. Prepárate para explicar cómo lo sabes.

    1. ¿Cuál número es mayor: \(\frac14\) o \(\frac54\)?
    2. ¿Cuál número está más lejos de 0: \(\frac14\) o \(\frac54\)?
    3. ¿Cuál número es mayor: \(\text{-}\frac {3}{4}\) o \(\frac58\)?
    4. ¿Cuál número está más lejos de 0: \(\text{-}\frac {3}{4}\) o \(\frac58\)?
    5. ¿El número que está más lejos del 0 siempre es el número mayor? Explica tu razonamiento.

Resumen

Usamos las palabras mayor que y menor que para comparar números en la recta numérica. Por ejemplo, los números -2.7, 0.8 y -1.3, se muestran en la recta numérica.

Number line, negative 3 to 3 by ones. Above the line, points are indicated at negative 2 point 7, negative 1 point 3, zero point 8.

Como -2.7 está a la izquierda de -1.3, decimos que -2.7 es menor que -1.3. Escribimos: \(\displaystyle \text-2.7 <\text -1.3\) En general, cualquier número que está a la izquierda de un número \(n\) es menor que \(n\).

Podemos ver que -1.3 es mayor que -2.7 porque -1.3 está a la derecha de -2.7. Escribimos: \(\displaystyle \text-1.3 >\text -2.7\) En general, cualquier número que está a la derecha de un número \(n\) es mayor que \(n\).

También podemos ver que \(0.8 > \text-1.3\) y \(0.8 > \text-2.7\). En general, cualquier número positivo es mayor que cualquier número negativo. 

Entradas del glosario

  • número negativo

    Un número negativo es un número que es menor que cero. En la recta numérica horizontal, los números negativos usualmente se muestran a la izquierda del 0.

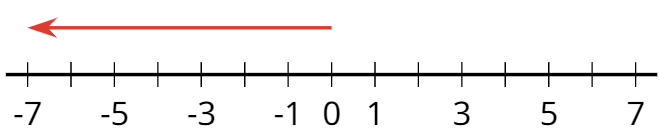
  • número positivo

    Un número positivo es un número que es mayor que cero. En la recta numérica horizontal, los números positivos usualmente se muestran a la derecha del 0.

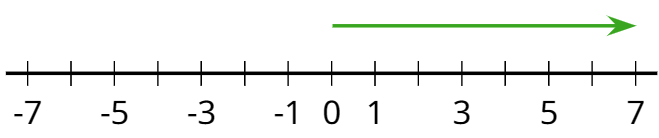
  • número racional

    Un número racional es una fracción o el opuesto de una fracción.

    Por ejemplo, 8 y -8 son números racionales porque se pueden escribir como  \(\frac81\) y \(\text-\frac81\).

    Los números 0.75 y -0.75 también son números racionales porque se pueden escribir como  \(\frac{75}{100}\) y \(\text-\frac{75}{100}\).

  • opuestos

    Dos números son opuestos si al ubicarlos sobre la recta numérica están a lados opuestos del 0 pero a la misma distancia del 0.

    Por ejemplo, 4 es el opuesto de -4 y -4 es el opuesto de 4. Ambos están a la misma distancia de 0. Uno de ellos es negativo y el otro es positivo.

    Number line that extends from -5 to 5, with points at -4 and 4.
  • signo

    El signo de cualquier número distinto de cero es positivo o negativo.

    Por ejemplo, el signo de 6 es positivo. El signo de -6 es negativo. El cero no tiene signo, porque no es positivo ni negativo.