Lección 11

Llenar recipientes

Llenemos un recipiente con agua.

Problema 1

Los cilindros A, B y C tienen el mismo radio pero diferentes alturas. Coloca los cilindros en orden de acuerdo a su volumen, del menor al mayor.

Three cylinders, A, B and C. No dimensions are given. Cylinder A is taller than Cylinder B. Cylinder C is taller than Cylinder B, and not as tall as Cylinder A

 

Problema 2

Dos cilindros, \(P\) y \(Q\), comenzaron cada uno con distintas cantidades de agua. La gráfica muestra cómo cambió la altura del agua a medida que el volumen del agua aumentó en cada cilindro. Empareja las gráficas de \(a\) y \(b\) a los cilindros P y Q. Explica tu razonamiento.

 

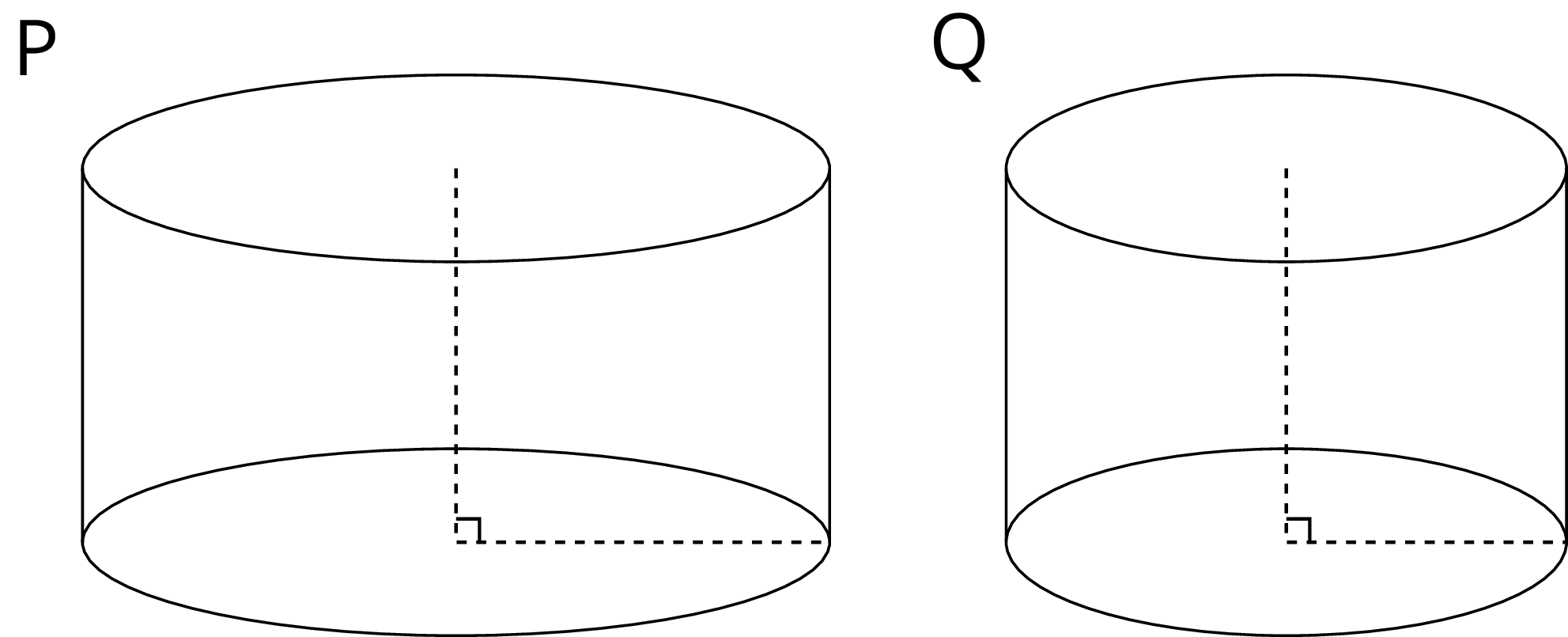
Problema 3

¿Cuál de las siguientes gráficas podría representar el volumen de agua en un cilindro como una función de su altura? Explica tu razonamiento.

Three graphs, all quadrant 1.  First, straight line, through origin, positive slope. Second, horizontal line begins above origin. Third, curve begins at origin, increases as it moves right.

 

Problema 4

La suma del área de los rectángulos es 30 centímetros cuadrados.

Two rectangles. First, 3 centimeters by x centimeters. Second, y centimeters by 2 centimeters.
  1. Escribe una ecuación que muestre la relación entre \(x\) y \(y\).
  2. Completa la tabla con los valores que faltan.
    \(x\) 3 8 12
    \(y\) 5 10
(de la Unidad 5, Lección 3.)