Lección 2
Representemos razones con diagramas
Usemos diagramas para representar razones.
2.1: Conversación numérica: dividir entre 4 y multiplicar por $\frac{1}{4}$
Encuentra mentalmente el valor de cada expresión.
\(24 \div 4\)
\(\frac{1}{4} \boldcdot 24\)
\(24\boldcdot \frac{1}{4}\)
\(5 \div 4\)
2.2: Una colección de cubos encajables
Esta es una colección de cubos encajables.

- Escoge dos de los colores en la foto y dibuja un diagrama que muestre el número de cubos encajables de cada uno de estos dos colores.
- Intercambia tu hoja con la de un compañero. En su hoja, escribe una frase que describa la razón que se muestra en su diagrama. Tu compañero hará lo mismo con tu diagrama.
- Devuelve la hoja a tu compañero. Lee la frase que tu compañero escribió en tu hoja. Si no estás de acuerdo, explica tu razonamiento.
2.3: Pintura azul y pasta para manualidades
Elena mezcló 2 tazas de pintura blanca con 6 cucharadas de pintura azul.
Este es un diagrama que representa esta situación.

-
Discutan cada afirmación y marquen todas las que describan la situación correctamente. Asegúrense de que ambos estén de acuerdo en cada respuesta que marquen.
- La razón de tazas de pintura blanca a cucharadas de pintura azul es \(2 : 6\).
- Por cada taza de pintura blanca, hay 2 cucharadas de pintura azul.
- Hay 1 taza de pintura blanca por cada 3 cucharadas de pintura azul.
- Hay 3 cucharadas de pintura azul por cada taza de pintura blanca.
- Por cada cucharada de pintura azul, hay 3 tazas de pintura blanca.
- Por cada 6 cucharadas de pintura azul, hay 2 tazas de pintura blanca.
- La razón de cucharadas de pintura azul a tazas de pintura blanca es de 6 a 2.
-
Jada mezcló 8 tazas de harina con 2 pintas de agua con el fin de hacer la pasta para el proyecto de arte.
-
Dibujen un diagrama que represente la situación.
- Escriban por lo menos dos afirmaciones que describan la razón de harina a agua.
-
2.4: Clasificación de tarjetas: salsa de espagueti
Tu profesor te dará tarjetas con varias recetas de salsa de espagueti. En los diagramas:
- Un círculo representa una taza de salsa de tomate
- Un cuadrado representa una cucharada de aceite
- Un triángulo representa una cucharadita de orégano

-
Túrnate con tu compañero para emparejar una afirmación con un diagrama.
- Para cada pareja que encuentres, explica a tu compañero cómo sabes que la afirmación y el diagrama forman una pareja.
- Para cada pareja que tu compañero encuentre, escucha con atención su explicación. Si no estás de acuerdo, discute tu razonamiento y traten de llegar a un acuerdo.
- Cuando tú y tu compañero estén de acuerdo en todas las parejas, comparen sus respuestas con la hoja de respuestas. Si hay algún error, discutan por qué y revisen sus parejas.
-
Había dos diagramas que podían ser pareja de dos afirmaciones diferentes. ¿Cuáles eran?
- El diagrama _______ se emparejaba con las afirmaciones ______ y ______.
- El diagrama _______ se emparejaba con las afirmaciones ______ y ______.
- Elige uno de los otros diagramas y crea otra afirmación que describa la razón que muestra el diagrama.
Escoge una receta y crea un diagrama que represente cualquiera de las razones en ella. ¿Es posible que incluyas más de 2 ingredientes en tu diagrama?
Resumen
Las razones se pueden representar usando diagramas. Los diagramas no necesitan tener detalles realistas. Por ejemplo, una receta de limonada dice: "Mezcle 2 cucharadas de polvo de limonada con 6 tazas de agua".
En lugar de esto:

Podemos dibujar algo así:

Este diagrama muestra que la razón de tazas de agua a cucharadas de polvo de limonada es 6 a 2. También podemos ver que por cada cucharada de polvo de limonada, hay 3 tazas de agua.
Entradas del glosario
- razón
Una razón es una asociación entre dos o más cantidades.
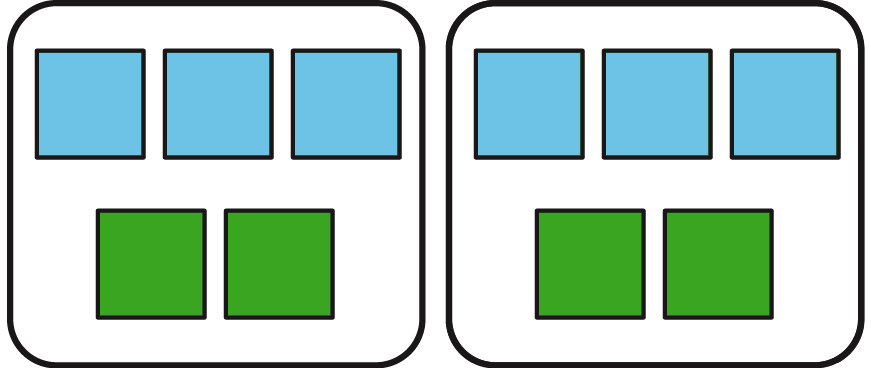
Por ejemplo, la razón \(3:2\) podría describir una receta que usa 3 tazas de harina por cada 2 huevos, o un bote que recorre 3 metros cada 2 segundos. Una forma de representar la razón \(3:2\) es con un diagrama que tiene 3 cuadrados azules por cada 2 cuadrados verdes.