Lección 5

El tamaño del factor de escala

Veamos qué efectos tienen los diferentes factores de escala.

5.1: Conversación numérica: factor desconocido

Resuelve mentalmente cada ecuación.

\(16x=176\)

\(16x=8\)

\(16x=1\)

\(\frac15x=1\)

\(\frac25x=1\)

5.2: Clasificación de tarjetas: copias a escala

Tu profesor te dará un grupo de tarjetas. En cada tarjeta, la figura A es la original y la figura B es la copia a escala.

  1. Clasifica las tarjetas con base en sus factores de escala. Prepárate para explicar tu razonamiento.

  2. Analiza las tarjetas 10 y 13 con más atención. ¿Qué observas sobre las figuras y tamaños de las figuras? ¿Qué observas sobre los factores de escala?

  3. Analiza las tarjetas 8 y 12 con más atención. ¿Qué observas sobre las figuras? ¿Qué observas sobre los factores de escala?



El triángulo B es una copia a escala del triángulo A con factor de escala \(\frac12\).

  1. ¿Cuántas veces mayores son las longitudes de los lados del triángulo B cuando se comparan con las del triángulo A?
  2. Imagina que redimensionas el triángulo B según un factor de escala de \(\frac12\) para obtener el triángulo C. ¿Cuántas veces mayores serán las longitudes de los lados del triángulo C cuando se comparen con las del triángulo A?
  3. El triángulo B se ha redimensionado 1 vez. El triángulo C se ha redimensionado dos veces. Imagina que redimensionas el triángulo A \(n\) veces y obtienes el triángulo N, siempre usando un factor de escala de \(\frac12\). ¿Cuántas veces mayores serán las longitudes de los lados del triángulo N cuando se comparen con las del triángulo A?

5.3: Cambiemos la escala de un rompecabezas

Tu profesor te dará 2 piezas de un rompecabezas de 6 piezas. 

  1. Si dibujaras copias a escala de las piezas del rompecabezas usando un factor de escala de \(\frac12\), ¿serían más grandes o más pequeñas que las piezas originales? ¿Cómo lo sabes?
  2. Crea una copia a escala de cada pieza del rompecabezas sobre un cuadrado en blanco, con un factor de escala de \(\frac12\).
  3. Cuando todos en tu grupo hayan acabado, organicen las 6 piezas del rompecabezas original de a siguiente manera:
    A grid with 2 rows, 3 columns. First row is 1, 2, 3, and second row is 4, 5, 6.
    Después pongan las 6 copias a escala juntas. Comparen el rompecabezas a escala con el rompecabezas original. ¿Qué partes parecen estar redimensionadas correctamente y cuáles parecen estar mal? ¿Qué puede haber hecho que esas partes estén mal?
  4. Revisen cualquier copia a escala que se pueda haber dibujado de forma incorrecta. 
  5. Si perdieran una de las piezas del rompecabezas original, pero aún tuviesen la copia a escala, ¿cómo podrían crear de nuevo la pieza perdida?

5.4: Figura, factor o copia desconocidos

  1. ¿Cuál es el factor de escala que lleva el triángulo original a su copia? Explica o muestra tu razonamiento. 

  2. El factor de escala que lleva el trapecio original a su copia es 2. Dibuja la copia a escala. 

  3. El factor de escala que lleva la figura original a su copia es \(\frac32\). Dibuja la figura original.
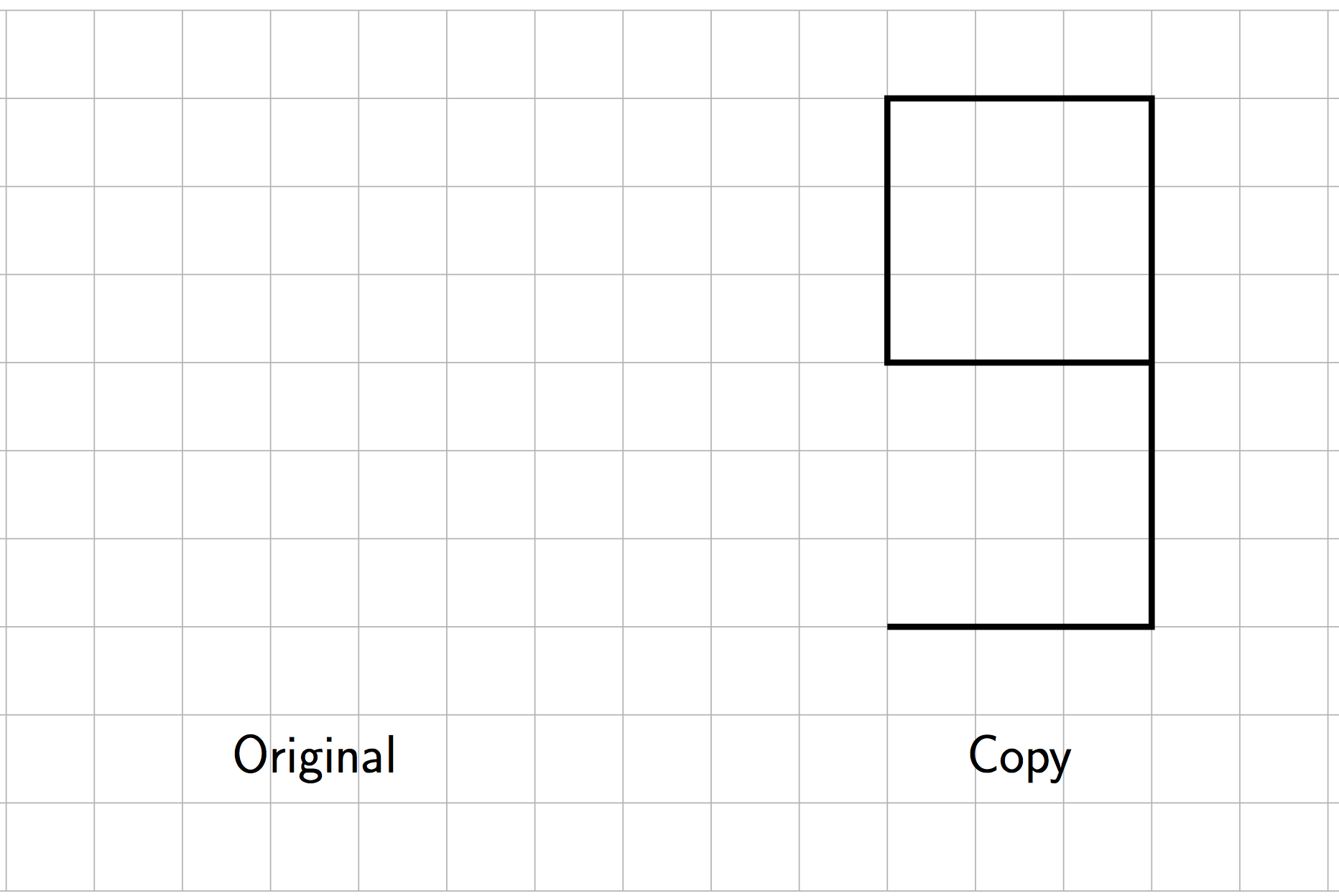
    Original needs to be drawn. The copy is on a grid and shaped like a 9 with an overall height of 6. The top of the 9 is the outline of a 3 by 3 box. The bottom horizontal is 3 units.
  4. ¿Cuál es el factor de escala que lleva el triángulo original a su copia? Explica por qué lo sabes.
  5. El factor de escala que lleva la figura original a su copia es 3. Dibuja la copia a escala.

Resumen

El tamaño del factor de escala afecta el tamaño de la copia. Cuando una figura se redimensiona por un factor de escala mayor que 1, la copia es más grande que la original. Cuando el factor de escala es menor que 1, la copia es más pequeña. Cuando el factor de escala es exactamente 1, la copia tiene el mismo tamaño que la original.

El triángulo \(DEF\) es una copia a escala más grande que el triángulo \(ABC\), porque el factor de escala de \(ABC\) a \(DEF\) es \(\frac32\). El triángulo \(ABC\) es una copia a escala más pequeña que el triángulo \(DEF\), porque el factor de escala de \(DEF\) a \(ABC\) es \(\frac23\).

Two triangles; one labeled A B C with horizontal A B and the other D E F with horizontal D E. 

Esto significa que los triángulos \(ABC\) y \(DEF\) son copias a escala uno del otro. Esto también muestra que el redimensionamiento se puede revertir usando factores recíprocos como \(\frac23\) y \(\frac32\).

En otras palabras, si redimensionamos la figura A usando un factor de escala de 4 para crear la figura B, podemos redimensionar la figura B usando el factor de escala recíproco, \(\frac14\), para crear la figura A.

Entradas del glosario

  • copia a escala

    Una copia a escala es una copia de una figura en la cual cada longitud de la figura original se multiplica por el mismo número.

    Por ejemplo, el triángulo \(DEF\) es una copia a escala del triángulo \(ABC\). Cada longitud de lado en el triángulo \(ABC\) fue multiplicada por 1.5 para obtener la longitud de lado correspondiente en el triángulo \(DEF\).

    2 triangles
  • correspondiente

    Si una parte de una figura y una parte de una copia de la figura están en la misma posición en relación a las demás partes de cada figura, decimos que las partes son correspondientes. Estas partes pueden ser puntos, segmentos, ángulos o distancias.

    Por ejemplo, el punto en \(B\) el primer triángulo corresponde al punto \(E\) en el segundo triángulo.

    El segmento \(AC\) corresponde al segmento \(DF\).

    2 triangles with corresponding parts
  • factor de escala

    Para crear una copia a escala, multiplicamos todas las longitudes de la figura original por el mismo número. Ese número se llama el factor de escala.

    En este ejemplo, el factor de escala es 1.5, porque \(4 \boldcdot (1.5) = 6\), \(5 \boldcdot (1.5)=7.5\), and \(6 \boldcdot (1.5)=9\).

    2 triangles
  • recíproco

    Al dividir 1 entre un número, se obtiene el recíproco de ese número. Por ejemplo, el recíproco de 12 es \(\frac{1}{12}\) y el recíproco de \(\frac25\) es \(\frac52\).