Lección 14
Encontremos soluciones a desigualdades en un contexto
Resolvamos desigualdades más complicadas.
Problema 1
La solución de \(5-3x > 35\) puede ser \(x>\text-10\) o \(\text-10>x\). ¿Cuál solución es correcta? Explica cómo lo sabes.
Problema 2
El director de la banda escolar sabe por experiencia previa que si cobran \(t\) dólares por una entrada al concierto, pueden esperar una asistencia de \(1000-50t\) personas. El director usó este modelo para concluir que el precio de un boleto debe ser \$8 o más para que asistan al menos 600 personas. ¿Estás de acuerdo con esta afirmación? ¿Por qué o por qué no?
Problema 3
¿Cuál desigualdad es verdadera cuando el valor de \(x\) es -3?
\(\text-x -6 < \text-3.5\)
\(\text-x- 6 >3.5\)
\(\text-x -6 > \text-3.5\)
\(x -6 > \text-3.5\)
Problema 4
Dibuja el conjunto solución de cada una de las siguientes desigualdades.
-
\(x\leq5\)
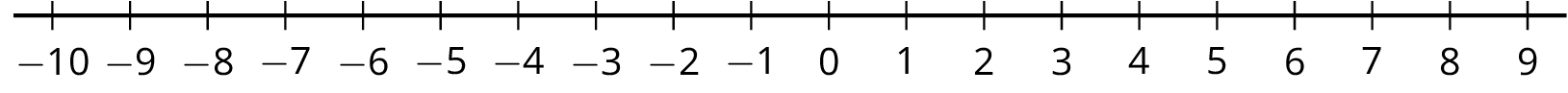
-
\(x<\frac52\)
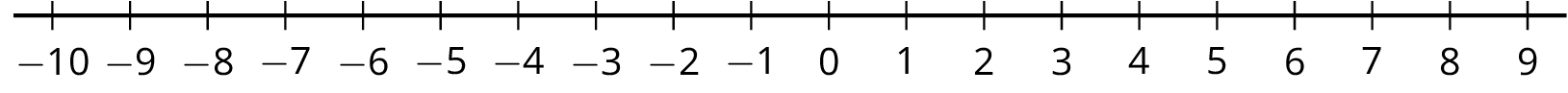
Problema 5
Escribe tres ecuaciones distintas que correspondan con el diagrama de cinta.

Problema 6
Un panadero quiere reducir la cantidad de azúcar en sus recetas de pasteles. Decide reducir la cantidad que usa en 1 pastel en \(\frac12\) taza. Después, él usa \(4\frac12\) tazas de azúcar para hornear 6 pasteles.
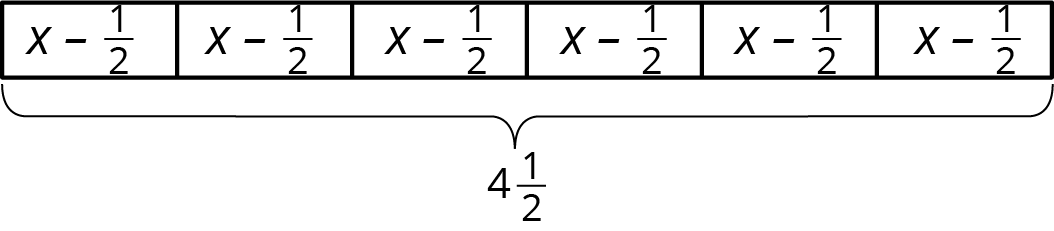
- Describe cómo el diagrama de cinta representa la historia.
- ¿Cuánto azúcar había originalmente en cada receta del pastel?
Problema 7
Hace un año, Clare medía 4 pies y 6 pulgadas de alto. Ahora, Clare mide 4 pies y 10 pulgadas de alto. ¿En qué porcentaje aumentó la estatura de Clare en el último año?