Lección 15

Resolvamos desigualdades de forma eficiente

Resolvamos desigualdades más complicadas.

Problema 1

  1. Considera la desigualdad \(\text-1 \leq \frac{x}{2}\).
    1. Predice cuáles valores de \(x\) harán verdadera la desigualdad.
    2. Completa la tabla para verificar tu predicción.
      \(x\) -4 -3 -2 -1 0 1 2 3 4
      \(\frac{x}{2}\)
  2. Considera la desigualdad \(1 \leq \frac {\text{-}x}{2}\).
    1. Predice cuáles valores de \(x\) harán verdadera la desigualdad.
    2. Completa la tabla para verificar tu predicción.
      \(x\) -4 -3 -2 -1 0 1 2 3 4
      \(\text-\frac{x}{2}\)

Problema 2

Diego está resolviendo la desigualdad \(100-3x \ge \text-50\). Él resuelve la ecuación \(100-3x = \text-50\) y obtiene \(x=50\). ¿Cuál es la solución de la desigualdad? 

A:

\(x < 50\)

B:

\(x \le 50\)

C:

\(x > 50\)

D:

\(x \ge 50\)

Problema 3

Resuelve la desigualdad \(\text-5(x-1)>\text-40\) y grafica la solución en una recta numérica.

Problema 4

Selecciona todos los valores de \(x\) que hacen verdadera la desigualdad \(\text-x+6\ge10\).

A:

-3.9

B:

4

C:

-4.01

D:

-4

E:

4.01

F:

3.9

G:

0

H:

-7

(de la Unidad 6, Lección 13.)

Problema 5

Dibuja el conjunto solución de cada una de las siguientes desigualdades. 

  1. \(x>7\)

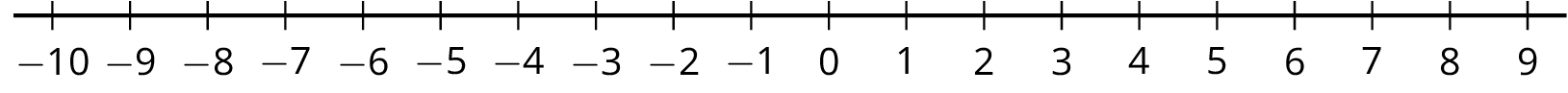
  2. \(x\geq\text-4.2\)

(de la Unidad 6, Lección 13.)

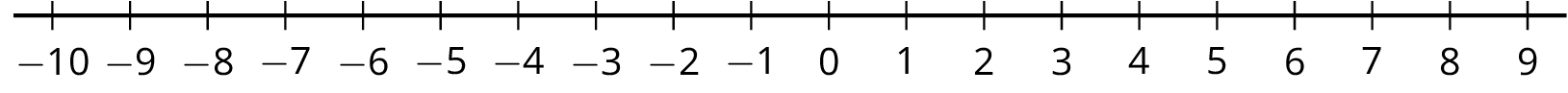
Problema 6

El precio de un par de aretes es \$22, pero Priya los compra en promoción por \$13.20.

  1. ¿Cuánto se descontó del precio?
  2. ¿Cuál fue el porcentaje del descuento?
(de la Unidad 4, Lección 12.)