Lección 2
Razonemos sobre contextos usando diagramas de cinta
Usemos diagramas de cinta para dar sentido a diferentes tipos de historias.
Problema 1
La tabla muestra el número de manzanas y el peso total de las manzanas.
| número de manzanas | peso de las manzanas (gramos) |
|---|---|
| 2 | 511 |
| 5 | 1200 |
| 8 | 2016 |
Estima el peso de 6 manzanas.
Problema 2
Elige todas las historias que el diagrama de cinta puede representar.
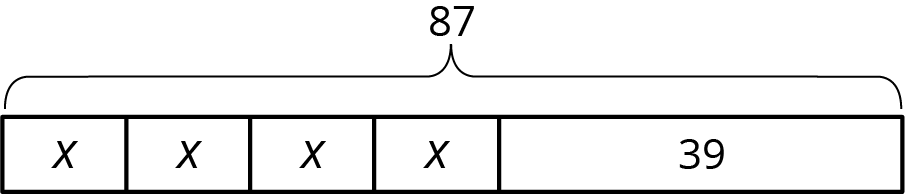
Hay 87 niños y 39 adultos en un espectáculo. Los asientos en el teatro están distribuidos en 4 secciones iguales.
Hay 87 estudiantes de los primeros grados en la guardería. Después de que recogen a 39 estudiantes, el profesor coloca al resto de los estudiantes en 4 grupos para una actividad.
Lin compra un paquete de 87 lápices. Le da 39 a su profesor y comparte los lápices restantes entre ella y sus 3 amigos.
Andre compra 4 paquetes de clips con 39 clips en cada uno. Luego le da 87 clips a su profesor.
La familia de Diego gasta \$87 en 4 tiquetes para la feria y $39 en una cena.
Problema 3
Andre quiere ahorrar \$40 y comprar con esto un regalo para su papá. El vecino de Andre le pagará semanalmente por cortar el césped, pero Andre siempre da una donación de $2 al banco de alimentos en las semanas en que gana dinero. Andre calcula que tardará 5 semanas en ganar el dinero para el regalo de su papá. Él dibuja un diagrama de cinta para representar la situación.
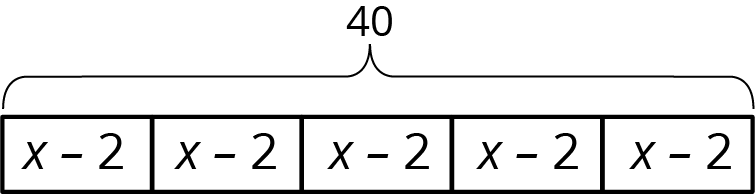
- Explica cómo las partes del diagrama de cinta representan la historia.
- ¿Cuánto le paga el vecino a Andre por cortar el césped cada semana?
Problema 4
Sin evaluar cada expresión, decide qué valor es el mayor. Explica cómo lo sabes.
- \(7\frac56 - 9\frac34\)
- \((\text-7\frac56) + (\text-9\frac34)\)
- \((\text-7\frac56) \boldcdot 9\frac34\)
- \((\text-7\frac56) \div (\text-9\frac34)\)
Problema 5
Resuelve cada ecuación.
- \((8.5) \boldcdot (\text-3) = a\)
- \((\text-7) + b = (\text-11)\)
- \(c - (\text-3) = 15\)
- \(d \boldcdot (\text-4) = 32\)