Lección 3

Razonemos sobre ecuaciones usando diagramas de cinta

Veamos cómo las ecuaciones pueden describir diagramas de cinta.

Problema 1

Resuelve mentalmente cada ecuación.

  1. \(2x = 10\)
  2. \(\text-3x = 21\)
  3. \(\frac13 x = 6\)
  4. \(\text-\frac12x = \text-7\)
(de la Unidad 5, Lección 15.)

Problema 2

Completa los cuadrados mágicos de manera que la suma de cada fila, cada columna y cada diagonal en la cuadrícula sean todas iguales.​

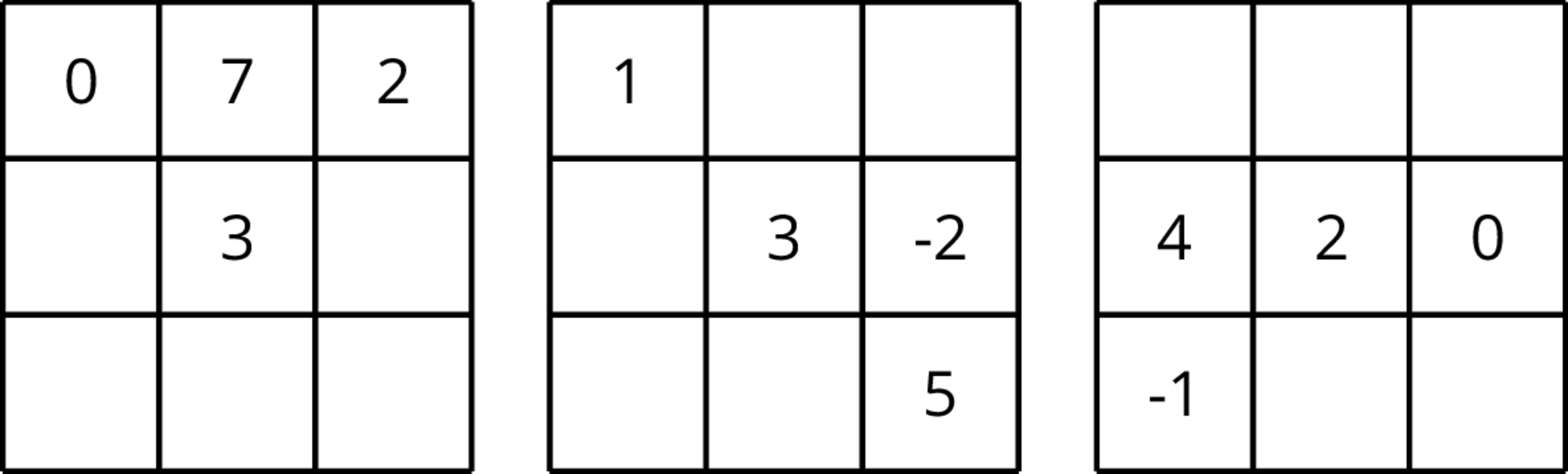
Three square grids, each with three columns and three rows. Square grid 1 is populated as follows: Row 1: 0, 7, 2. Row 2: blank, 3, blank. Row 3: blank, blank, blank. Square grid 2 is populated as follows: Row 1: 1, blank, blank. Row 2: blank, 3, negative 2. Row 3: blank, blank, five. Square grid 3 is populated as follows: Row 1: Blank, blank, blank. Row 2: 4, 2, 0. Row 3: negative 1, blank, blank.
(de la Unidad 5, Lección 3.)

Problema 3

Dibuja un diagrama de cinta que corresponda con cada ecuación.

  1. \(5(x+1)=20\)

  2. \(5x+1=20\)

Problema 4

Selecciona todas las ecuaciones que correspondan con el diagrama de cinta.

A:

\(35=8+x+x+x+x+x+x\)

B:

\(35=8+6x\)

C:

\(6+8x=35\)

D:

\(6x+8=35\)

E:

\(6x+8x=35x\)

F:

\(35-8=6x\)

Problema 5

Cada automóvil viaja a una velocidad constante. Encuentra cuántas millas viaja cada automóvil en 1 hora a la tasa indicada.

  1. 135 milas en 3 horas

  2. 22 millas en \(\frac12\) hora

  3. 7.5 millas en \(\frac14\) hora

  4. \(\frac{100}{3}\) millas en \(\frac23\) hora

  5. \(97\frac12\) millas en \(\frac32\) hora

(de la Unidad 4, Lección 2.)