Lección 6
Distingamos entre dos tipos de situaciones
Pensemos en ecuaciones con y sin paréntesis y los tipos de situaciones que describen.
Problema 1
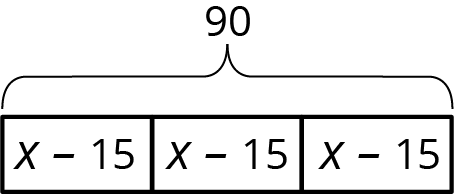
Una escuela pidió 3 cajas grandes de marcadores para tablero. Después de darle 15 marcadores a cada uno de los 3 profesores, quedaron 90 marcadores. El diagrama representa la situación. ¿Cuántos marcadores había originalmente en cada caja?
Problema 2
El diagrama se puede representar con la ecuación \(25=2+6x\). Explica dónde puedes ver el 6 en el diagrama.

Problema 3
Empareja cada ecuación con una historia. (Dos de las historias se emparejan con la misma ecuación.)
- \(3(x+5)=17\)
- \(3x+5=17\)
- \(5(x+3)=17\)
- \(5x+3=17\)
- El profesor de Jada llena una maleta de viaje con 5 copias de un libro. El peso total de la bolsa y los libros es de 17 libras. La bolsa vacía pesa 3 libras. ¿Cuánto pesa cada libro?
- Una parte del escenario para la obra de teatro escolar tiene una forma rectangular de 5 pies de largo. El diseñador decide incrementar el largo de la pieza. En el escenario habrá 3 rectángulos iguales con largo total de 17 pies. ¿En cuánto aumentó el diseñador la longitud de cada rectángulo?
- Elena gasta \$17, ella compra un libro que cuesta \$3 y un marcador para cada uno de sus 5 primos. ¿Cuánto cuesta cada marcador?
- Noah empaca bolsas en la despensa de alimentos para entregar a las familias. Él empaca 5 bolsas, las cuales tienen un peso total de 17 libras. Cada bolsa contiene 3 libras de provisiones y un paquete de documentos con información sobre salud. ¿Cuánto pesa cada paquete de documentos?
- Andre tiene 3 veces la cantidad de lápices de Noah y 5 bolígrafos. Él tiene en total 17 objetos entre bolígrafos y lápices. ¿Cuántos lápices tiene Noah?
Problema 4
Elena caminó 20 minutos más que Lin. Jada caminó el doble de lo que Elena caminó. Jada caminó durante 90 minutos. La ecuación \(2(x+20)=90\) describe esta situación. Empareja cada cantidad en la historia con la expresión que represente.