Lección 7
Razonemos sobre la resolución de ecuaciones (Parte 1)
Veamos en qué se parece un colgador balanceado a una ecuación y cómo mover sus pesos es parecido a resolver la ecuación.
Problema 1
Existe una relación proporcional entre el volumen de una muestra de helio en litros y la masa de esa muestra en gramos. Si la masa de una muestra es 5 gramos, su volumen es 28 litros. \((5, 28)\) se muestra en la gráfica siguiente.
- ¿Cuál es la constante de proporcionalidad en esta relación?
- En esta situación, ¿cuál es el significado del número que encontraste en la pregunta anterior?
- Agrega por lo menos tres puntos más a la gráfica y etiquétalos con sus coordenadas.
- Escribe una ecuación que muestre la relación entre la masa de una muestra de helio y su volumen. Utiliza \(m\) para masa y \(v\) para volumen.
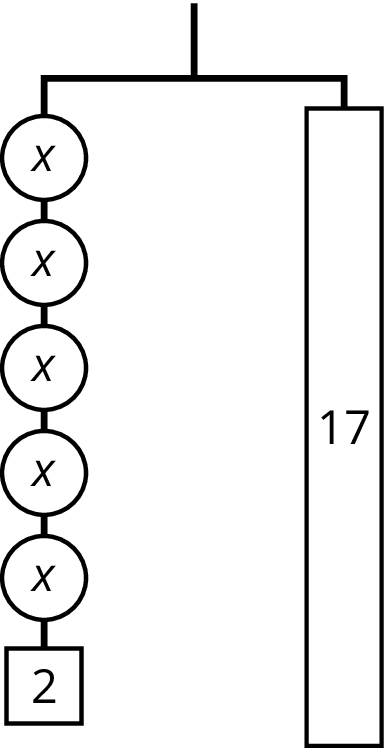
Problema 2
Explica cómo las partes del colgador balanceado se asocian con las partes de la ecuación.
\(7=2x+3\)
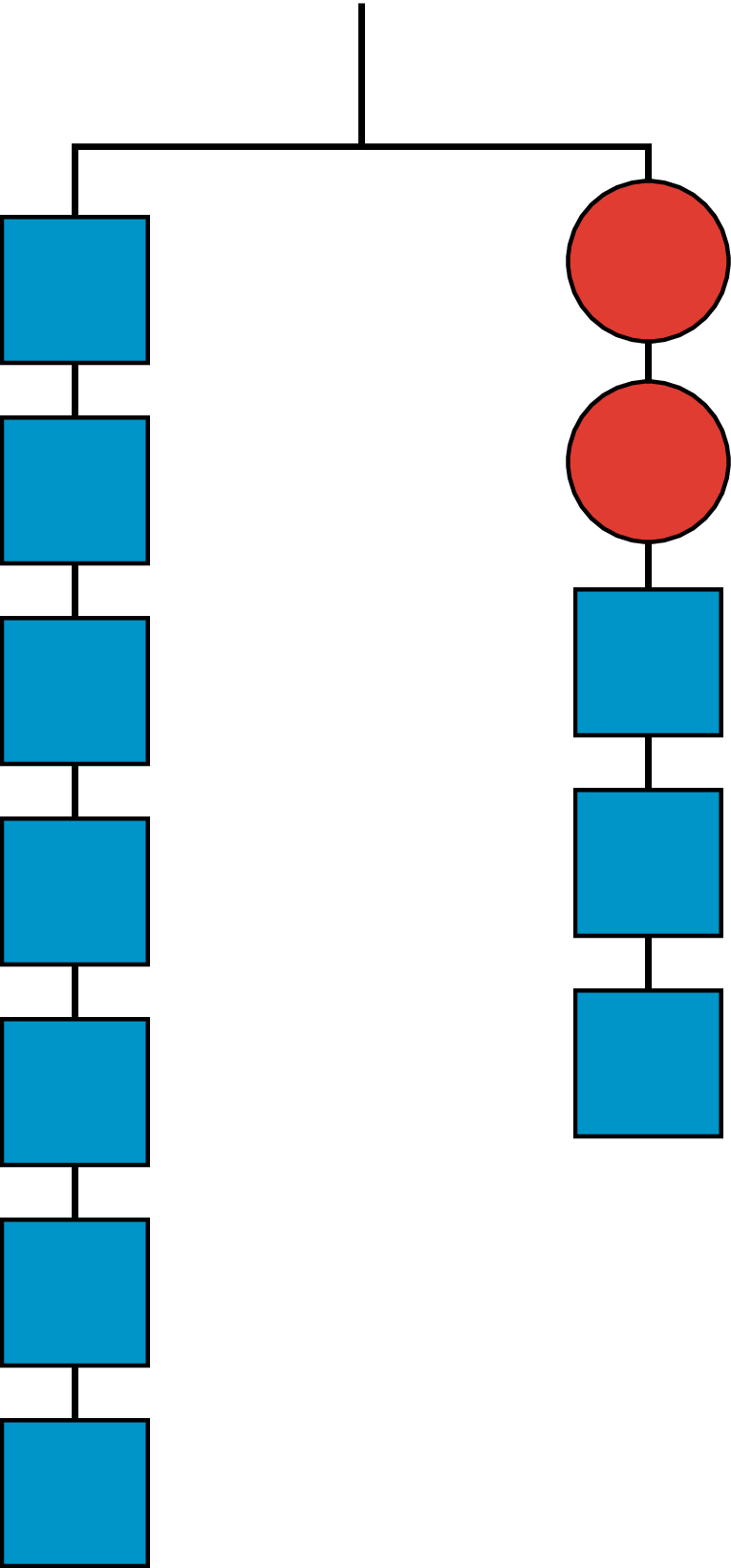
Problema 3
Este es un colgador:
- Escribe una ecuación para representar el colgador.
- Dibuja más colgadores para mostrar cada paso que harías para hallar \(x\). Explica tu razonamiento.
- Escribe una ecuación para describir cada uno de los colgadores que dibujaste. Describe cómo cada ecuación coincide con su colgador.