Lección 6
Estimemos probabilidades utilizando simulación
Simulemos situaciones del mundo real.
6.1: Cuál es diferente: ruletas
¿Cuál ruleta es diferente?
6.2: La caminata de Diego
Tu profesor le dará a tu grupo los materiales necesarios para hacer una de tres simulaciones diferentes. Sigue estas instrucciones para simular la caminata de Diego durante 15 días. Los primeros 3 días ya están hechos para ti.
- Simula un día:
-
Si a tu grupo le dieron una bolsa con papeles, saca un papel sin mirar adentro.
-
Si a tu grupo le dieron una ruleta, hazla girar y mira dónde para.
-
Si a tu grupo le dieron dos dados numéricos, lanza ambos dados y suma los números en los que cayeron. Si la suma es un valor de 2 a 8, esto significa que Diego debe esperar.
-
-
Anota en la tabla si Diego tuvo o no tuvo que esperar más de 1 minuto.
-
Calcula el total del número de días y la fracción acumulada de días que Diego ha tenido que esperar hasta el momento.
-
En la gráfica, ubica el número de días y la fracción que Diego ha tenido que esperar. Une los puntos con rectas.
-
Si tu grupo tiene la bolsa con los papeles, pon el papel nuevamente dentro de la bolsa y agítala para mezclar los papeles.
-
Pasa los implementos a la siguiente persona del grupo.
| día | ¿Diego tiene que esperar más de 1 minuto? |
número total de días que Diego tuvo que esperar |
fracción de días que Diego tuvo que esperar |
|---|---|---|---|
| 1 | no | 0 | \(\frac{0}{1} =\) 0.00 |
| 2 | sí | 1 | \(\frac{1}{2} =\) 0.50 |
| 3 | sí | 2 | \(\frac{2}{3} \approx\) 0.67 |
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 | |||
| 12 | |||
| 13 | |||
| 14 | |||
| 15 |
-
Basándote en los datos que recogiste, ¿crees que la fracción de días que Diego tiene que esperar después del 16º día estará más cerca de 0.9 o de 0.7? Explica o muestra tu razonamiento.
-
Continúa la simulación por otros 10 días. Registra tus resultados en esta tabla y en la gráfica anterior.
día ¿Diego tiene que
esperar más
de 1 minuto?número total de
días que Diego
tuvo que esperarfracción de
días que Diego
tuvo que esperar16 17 18 19 20 21 22 23 24 25 - ¿Qué observas acerca de la gráfica?
- Basándote en la gráfica, estima la probabilidad de que Diego tenga que esperar más de 1 minuto para cruzar por el cruce peatonal.
Veamos por qué los valores tienden a no cambiar mucho después de hacer la simulación muchas veces.
-
Después de realizar la simulación 4 veces, un grupo se da cuenta de que Diego tuvo que esperar 3 veces. Con base en estos resultados, ¿cuál es una estimación para la probabilidad de que Diego tenga que esperar?
- Si este grupo realiza la simulación 1 vez más, ¿cuáles son los dos posibles resultados para la quinta simulación?
- Para cada posibilidad, estima la probabilidad de que Diego tenga que esperar.
- ¿Cuáles son las diferencias entre las posibles estimaciones después de hacer 5 simulaciones y la estimación después de 4 simulaciones?
-
Al hacer la simulación 20 veces, este grupo se da cuenta de que Diego tuvo que esperar 15 veces. Con base en estos resultados, ¿cuál es una estimación para la probabilidad de que Diego tenga que esperar?
- Si este grupo realiza la simulación 1 vez más, ¿cuáles son los dos posibles resultados para la simulación número veintiuno?
- Para cada posibilidad, estima la probabilidad de que Diego tenga que esperar.
- ¿Cuáles son las diferencias entre las posibles estimaciones después de 21 simulaciones y la estimación después 20 simulaciones?
-
Utiliza estos resultados para explicar por qué un solo resultado, después de hacer muchas simulaciones, no influye en la estimación tanto como lo hace un solo resultado al haber hecho solamente unas cuantas simulaciones.
6.3: Diseñemos experimentos
Para cada situación, describe un experimento de azar que podría representarla apropiadamente.
-
Seis personas van a almorzar juntas. Una de ellas será elegida aleatoriamente para que escoja a qué restaurante ir. ¿A quién le toca escoger?
-
Después de que un robot se pone de pie, es igualmente probable que dé un paso hacia adelante con su pie izquierdo o que lo dé con su pie derecho. ¿Cuál pie utilizará para dar su primer paso?
-
En un juego de computadora hay tres túneles. Cada vez que el nivel comienza, la computadora escoge aleatoriamente uno de los túneles que lleva al castillo. ¿Cuál túnel es?
-
Tu escuela va a llevar 4 buses de estudiantes a una excursión. ¿Se te va a asignar el mismo bus en el que va a ir tu profesor de matemáticas?
Resumen
A veces es más fácil estimar una probabilidad realizando una simulación. Una simulación es un experimento que se parece a una situación del mundo real. Las simulaciones son útiles si recoger suficiente información para estimar la probabilidad de algún evento es difícil o necesita mucho tiempo.
Por ejemplo, imagina que Andre debe hacer un transbordo de un bus a otro para ir a su clase de música. La mayoría de las veces él hace el transbordo sin problemas, pero a veces el primer bus está retrasado y él pierde el segundo bus. Podríamos adaptar una simulación con tarjetas de papel en una bolsa. Cada tarjeta se marca con la hora a la que llega el primer bus a la parada donde hace el transbordo. Escogemos aleatoriamente tarjetas de la bolsa. Después de varias pruebas, calculamos la fracción de veces que Andre perdió el bus para estimar la probabilidad de que vaya a perder el bus en un día determinado.
Entradas del glosario
- aleatorio
Los resultados de un experimento de azar son aleatorios si todos son igualmente posibles.
- espacio muestral
El espacio muestral es la lista de todos los resultados posibles de un experimento de azar.
Por ejemplo, el espacio muestral de lanzar dos monedas es:
cara-cara sello-cara cara-sello sello-sello - evento
Un evento es un conjunto de uno o más resultados en un experimento de azar. Por ejemplo, al lanzar un dado numérico, hay seis resultados posibles.
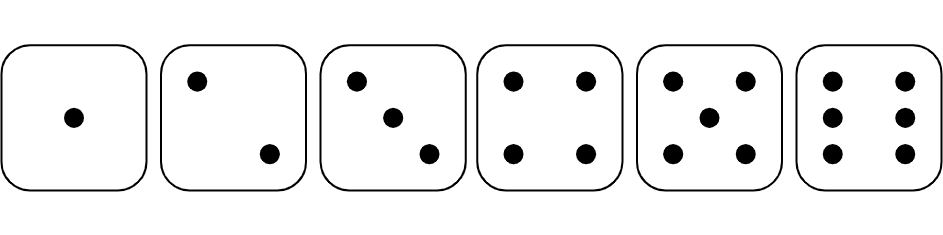
"Sacar un número menor a 3 al lanzar el dado", "sacar un número par al lanzar el dado" o "sacar 5 al lanzar el dado" son ejemplos de eventos.
- experimento de azar
Un experimento de azar es algo que puedes hacer una y otra vez, sin saber lo que va a ocurrir cada vez.
Por ejemplo, cada vez que haces girar una ruleta, puede caer en rojo ("R"), amarillo ("Y"), azul ("B") o verde ("G").
- probabilidad
La probabilidad de un evento es un número que nos indica qué tan posible es que suceda ese evento. Una probabilidad de 1 indica que el evento siempre sucede. Una probabilidad de 0 indica que el evento nunca sucede.
Por ejemplo, la probabilidad de sacar una ficha de esta bolsa (de forma aleatoria) y que sea una luna es \(\frac45\).
- resultado
Un resultado de un experimento de azar es una de las cosas que puede suceder cuando haces un experimento. Por ejemplo, los posibles resultados al lanzar una moneda son cara o sello.
- simulación
Una simulación es un experimento que se usa para estimar la probabilidad de un evento del mundo real.
Por ejemplo, supongamos que el pronóstico del tiempo dice que hay una probabilidad de 25% de lluvia. Podemos simular esta situación con una ruleta con cuatro secciones iguales. Si la ruleta cae en rojo, esto representa que llovió. Si la ruleta cae en cualquier otro color, esto representa que no llovió.