Lección 13

Descompongamos bases para calcular el área

Estudiemos cómo algunas personas usan el volumen.

Problema 1

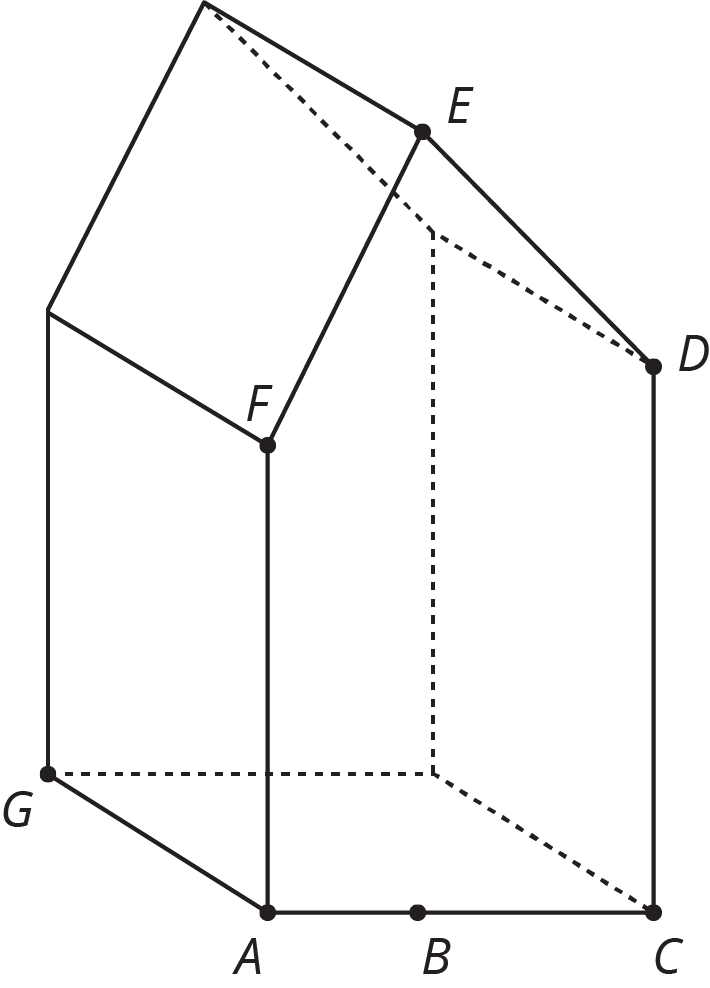
Te encuentras un cristal en la forma de un prisma. Halla el volumen del cristal.

El punto \(B\) está directamente debajo del punto \(E\), y las siguientes longitudes se conocen:

  • De \(A\) a \(B\): 2 mm
  • De \(B\) a \(C\): 3 mm
  • De \(A\) a \(F\): 6 mm
  • De \(B\) a \(E\): 10 mm
  • De \(C\) a \(D\): 7 mm
  • De \(A\) a \(G\): 4 mm

 

Problema 2

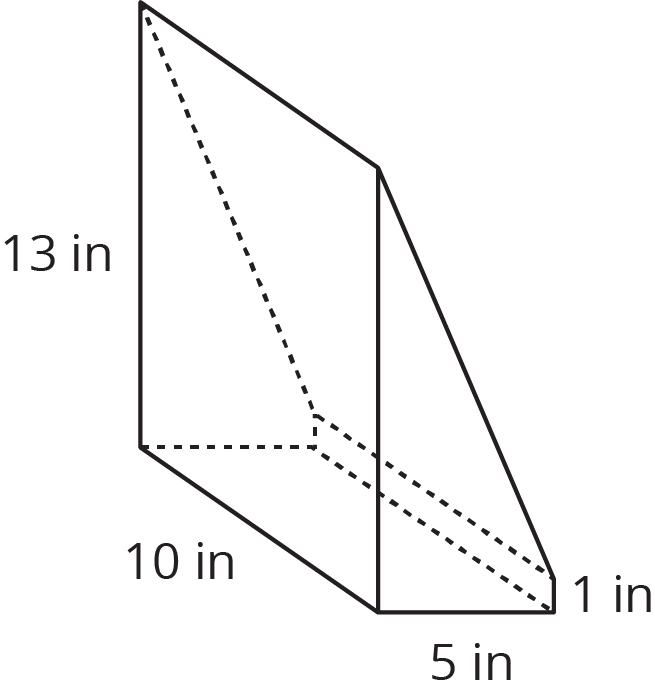
Un prisma rectangular con dimensiones 5 pulgadas por 13 pulgadas por 10 pulgadas se corta para obtener una pieza como la que se muestra en la imagen. ¿Cuál es el volumen de esta pieza? ¿Cuál es el volumen de la otra pieza que no está en la imagen?

Problema 3

Un triángulo tiene un lado de 7 cm y otro lado de 3 cm.

  1. Dibuja este triángulo y marca las medidas dadas. (Si tienes dificultades, intenta usar un compás o cortar algunos popotes de esas longitudes).
  2. Dibuja otro triángulo con las mismas medidas que no sea idéntico a tu primer triángulo.
  3. Explica cómo puedes saber que no son idénticos.
(de la Unidad 7, Lección 9.)

Problema 4

Selecciona todas las ecuaciones que representen relaciones que haya entre los ángulos de la figura.

A:

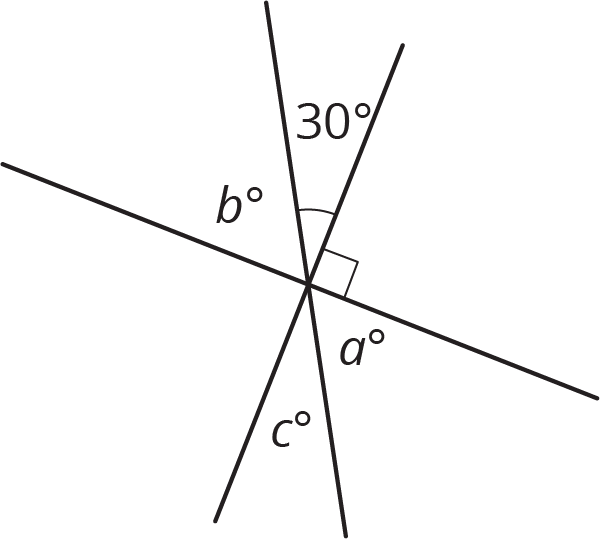
\(90-30=b\)

B:

\(30+b=a+c\)

C:

\(a+c+30+b=180\)

D:

\(a=30\)

E:

\(a=c=30\)

F:

\(90+a+c=180\)

(de la Unidad 7, Lección 4.)

Problema 5

Una mezcla de ponche contiene 1 cuarto de galón de jugo de limón, 2 tazas de jugo de uva, 4 cucharadas de miel y \(\frac12\) galón de agua con gas. Encuentra el porcentaje de la mezcla de ponche que proviene de cada ingrediente. Redondea tus respuestas al décimo de un porcentaje más cercano (una pista: 1 taza = 16 cucharadas).

(de la Unidad 4, Lección 9.)