Lección 3
Ángulos no adyacentes
Observemos ángulos que no están el uno al lado del otro.
Problema 1
Dos rectas se intersecan. Encuentra los valores de \(b\) y \(c\).
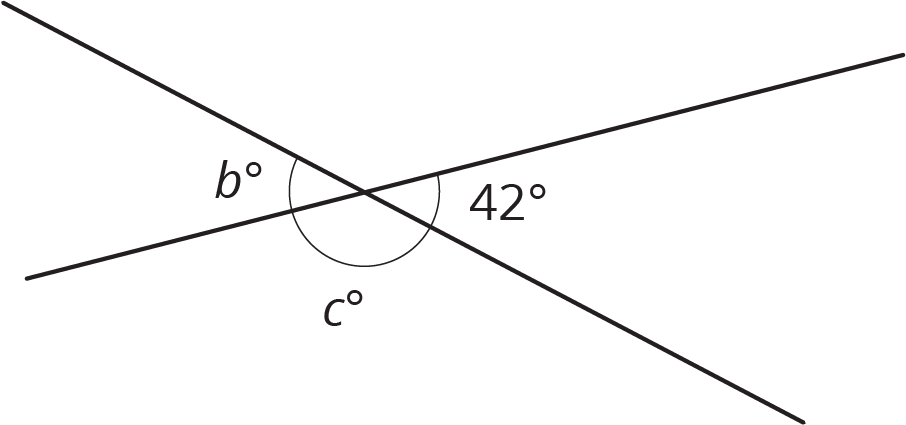
Problema 2
En esta figura, los ángulos \(R\) y \(S\) son complementarios. Encuentra la medida del ángulo \(S\).
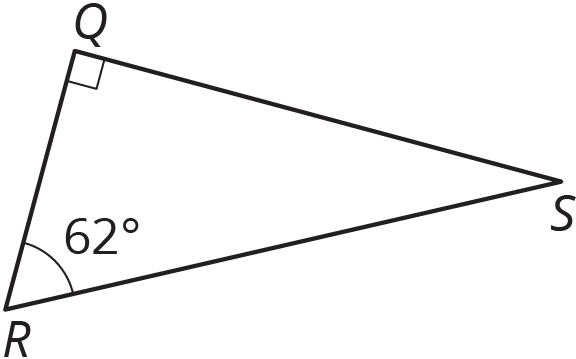
Problema 3
Si dos ángulos son opuestos y suplementarios, ¿se puede saber qué ángulos son? ¿Es posible que sean opuestos y complementarios? Si es así, ¿puedes determinar los ángulos? Explica cómo lo sabes.
Problema 4
Empareja cada expresión de la primera lista con una expresión equivalente de la segunda lista.
Problema 5
Factoriza cada expresión.
- \(15a-13a\)
- \(\text-6x-18y\)
- \(36abc+54ad\)
Problema 6
Los directores de un espectáculo de danza esperan que muchos estudiantes participen pero aún no saben cuántos estudiantes vendrán. Los directores necesitan que 7 estudiantes trabajen en el equipo técnico. El resto de los estudiantes trabajan en rutinas de baile, en grupos de 9. Para que el espectáculo funcione, necesitan que al menos 6 grupos completos trabajen en las rutinas de baile.
- Escribe y resuelve una desigualdad para representar esta situación y grafica la solución en una recta numérica.
- Escribe una oración para los directores sobre la cantidad de estudiantes que necesitan.
Problema 7
Un perro pequeño se alimenta con \(\frac{3}{4}\) taza de comida para perro dos veces al día. Si usamos \(d\) para el número de días y \(f\) para la cantidad de comida en tazas, escribe una ecuación que relacione las variables. Usa la ecuación para encontrar cuántos días durará una bolsa grande de comida para perro si contiene 210 tazas de comida.