Lección 4
Resolver para ángulos desconocidos
Determinemos algunos ángulos desconocidos.
Problema 1
\(M\) es un punto en el segmento de recta \(KL\). \(NM\) es un segmento de recta. Selecciona todas las ecuaciones que representen las relaciones que hay entre las medidas de los ángulos en la figura.
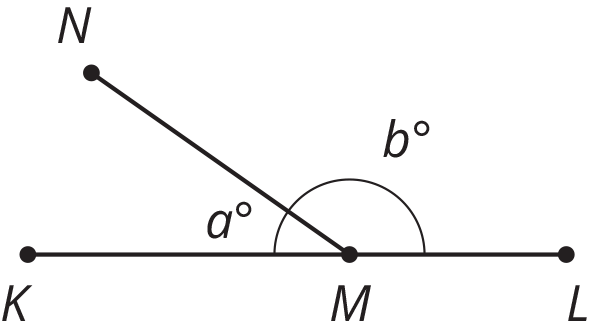
\(a=b\)
\(a+b=90\)
\(b=90-a\)
\(a+b=180\)
\(180-a=b\)
Problema 2
¿Cuál ecuación representa la relación entre los ángulos en la figura?
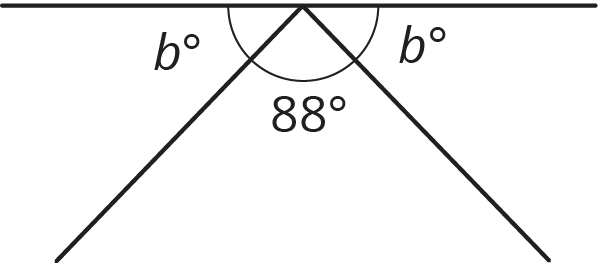
\(88+b=90\)
\(88+b=180\)
\(2b+88=90\)
\(2b+88=180\)
Problema 3
Los segmentos \(AB\), \(EF\) y \(CD\) se intersecan en el punto \(C\) y el ángulo \(ACD\) es un ángulo recto. Encuentra el valor de \(g\).
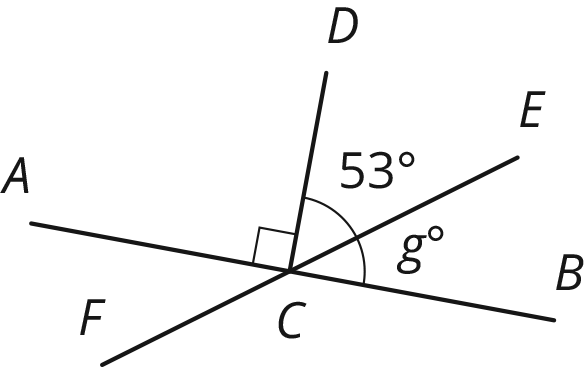
Problema 4
Selecciona todas las expresiones que son el resultado de disminuir \(x\) en un 80%.
\(\frac{20}{100}x\)
\(x - \frac{80}{100}x\)
\(\frac{100-20}{100}x\)
\(0.80x\)
\((1-0.8)x\)
Problema 5
Andre está resolviendo la ecuación \(4(x+\frac32)=7\). Él dice: "Puedo restar \(\frac32\) de cada lado para obtener \(4x=\frac{11}{2}\) y luego dividir entre 4 para obtener \(x=\frac{11}{8}\)". Kiran dice: "Creo que cometiste un error".
- ¿Cómo puede Kiran saber con certeza que la solución de Andre es incorrecta?
- Describe el error de Andre y explica cómo corregir su trabajo.
Problema 6
Resuelve cada ecuación.
\(\frac17a+\frac34=\frac98\)
\(\frac23+\frac15b=\frac56\)
\(\frac32=\frac43c+\frac23\)
\(0.3d+7.9=9.1\)
\(11.03=8.78+0.02e\)
Problema 7
Un tren recorre una larga distancia a una rapidez constante. Escribe las dos constantes de proporcionalidad para la relación entre la distancia recorrida y el tiempo transcurrido. Explica qué significa cada una.
| tiempo transcurrido (horas) | distancia (mi) |
|---|---|
| 1.2 | 54 |
| 3 | 135 |
| 4 | 180 |